Giải bài 55 trang 96 - Sách giáo khoa Toán 8 tập 1

Đề bài

 Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.

 

Hướng dẫn giải

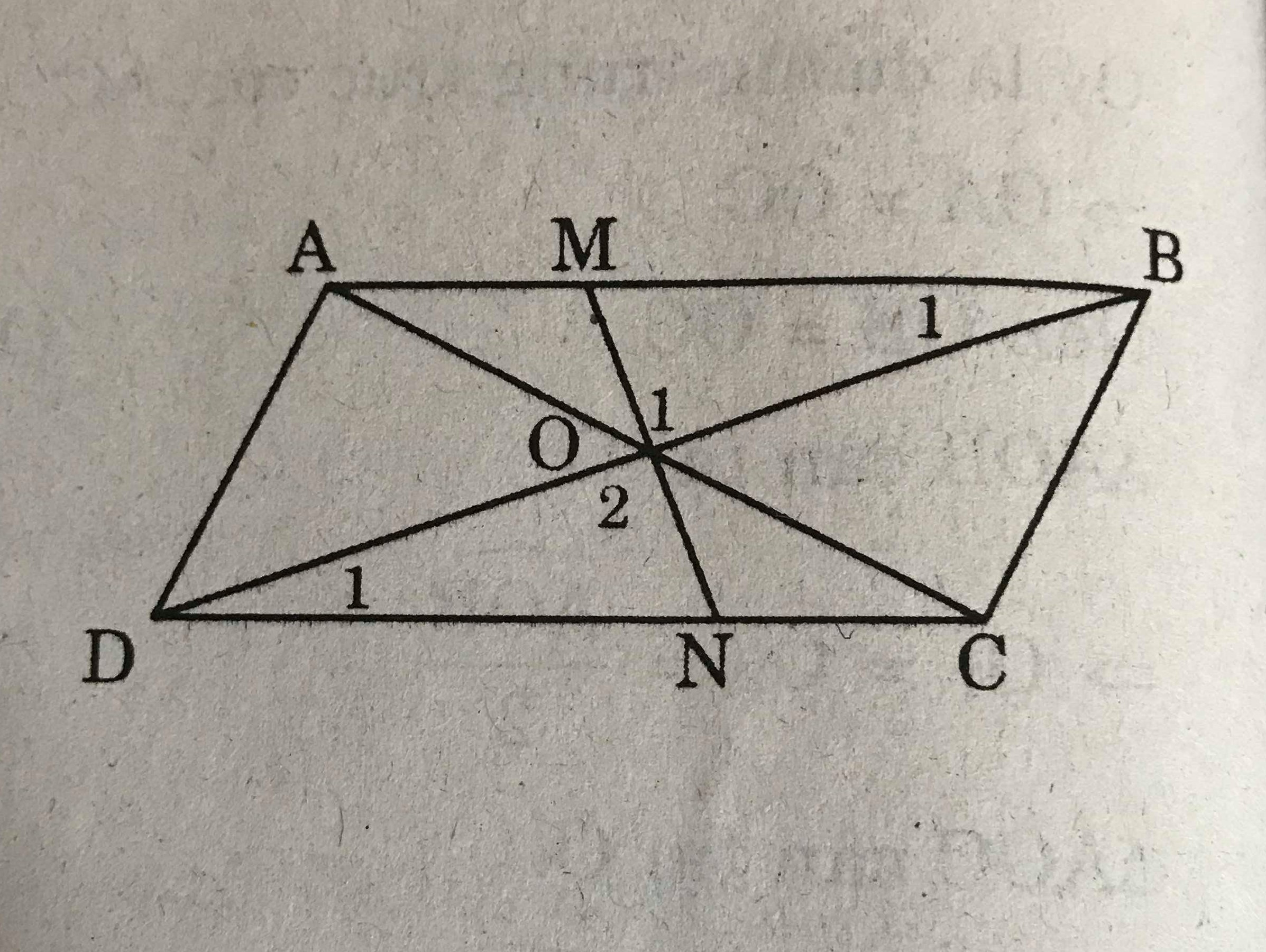
Xét ΔBOM và ΔDON có :

OB = OD (O là giao điểm của hai đường chéo hình bình hành).

\(\widehat{B_1}=\widehat{D_1}\) (hai góc so le trong của hai đường thẳng song song AB, CD)

\(\widehat{O_1}=\widehat{O_2}\) (đối đỉnh)

Nên  ΔBOM =  ΔDOM (g.c.g) => OM = ON

O là trung điểm của MN nên M đối xứng với N qua O.