Bài 16 trang 106 SGK Toán 9 tập 1

Đề bài

Cho đường tròn \((O)\), điểm \(A\) nằm bên trong đường tròn. Vẽ dây \(BC\) vuông góc với \(OA\) tại \(A\). Vẽ dây \(EF\) bất kì đi qua \(A\) và không vuông góc với \(OA\). Hãy so sánh độ dài hai dây \(BC\) và \(EF\).

Hướng dẫn giải

- Để so sánh hai dây, ta đi so sánh khoảng cách từ tâm đến hai dây đó.

- Sử dụng các tính chất sau:

+) Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

+) Trong một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Lời giải chi tiết

Vẽ \(OH\perp EF\).

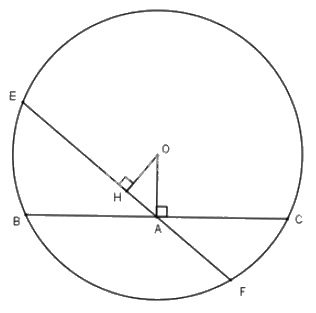
Để so sánh hai dây \(BC\) và \(EF\), ta đi so sánh hai khoảng cách \(OH\) và \(OA\).

Xét tam giác \(HOA\) vuông tại \(H\) suy ra \(OA\) là cạnh huyền.

Do đó \(OA > OH\).

Suy ra \(EF>BC.\)

Nhận xét. Trong các dây đi qua một điểm \(A\) ở trong đường tròn, dây vuông góc với \(OA\) là dây ngắn nhất.