Bài 1 trang 59 SGK Hình học 10

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\), \(\widehat{B}= 58^0\) và cạnh \(a = 72 cm\). Tính \(\widehat{C}\), cạnh \(b\), cạnh \(c\) và đường cao \(h_a\)

Hướng dẫn giải

+) Đỉnh lý tổng 3 góc trong một tam giác: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0.\)

+) Dựa vào công thức lượng giác của các góc nhọn trong tam giác vuông để làm tính các cạnh và chiều cao cần tìm của tam giác.

Lời giải chi tiết

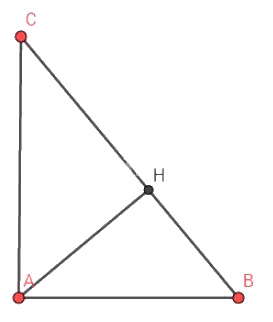
Theo định lí tổng \(3\) góc trong một tam giác ta có:

\(\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat C = {180^0} - \widehat A - \widehat B \cr&\;\;\;\;\;\;\;\;= {180^0} - {90^0} - {58^0} = {32^0} \cr} \)

Xét tam giác vuông \(ABC\) có:

\(b =a. \cos C= a.\cos {32^0} \)\(\Rightarrow b \approx 61,06cm\);        

\(c =a.\sin C= a.sin{32^0}\)\( \Rightarrow c \approx 38,15cm\)

 \(h_a =\frac{b.c}{a}\) \(\Rightarrow h_a ≈ 32,36cm.\)