Bài 10 trang 60 SGK Hình học 10

Đề bài

Hai chiếc tàu thủy \(P\) và \(Q\) cách nhau \(300m\).Từ \(P\) và \(Q\) thẳng hàng với chân \(A\) của tháp hải đăng \(AB\) ở trên bờ biển người ta nhìn chiều cao \(AB\) của tháp dưới các góc \(\widehat {BPA} = {35^0},\widehat {BQA} = {48^0}.\) Tính chiều cao của tháp.

Hướng dẫn giải

+) Dựa vào công thức lượng giác của các góc nhọn trong tam giác vuông.

Lời giải chi tiết

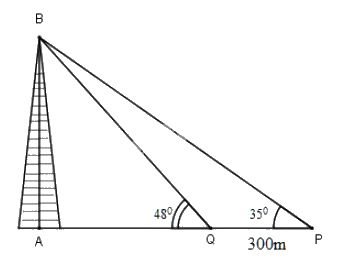
Ta có: \(\cot Q=\frac{AQ}{AB} \Rightarrow AQ = AB\cot48^0\) 

Tương tự có: \(AP = AB\cot35^0\) 

\(\Rightarrow QP =AP-AQ\)\(= AB(cot35^0- cot48^0)\) 

\(\Rightarrow AB = {{300} \over {\cot {{35}^0} - \cot {{48}^0}}} \approx {{300} \over {1,4281 - 0,9004}} \)\(\approx 568,457m.\)