30 bài tập trắc nghiệm sự đồng biến nghịch biến củ...
- Câu 1 : Hàm số
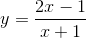đồng biến trên A R
B R\{-1}
C \(\left( { - \infty ;-1} \right)\) và \(\left( {-1; + \infty } \right)\)
D
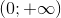
- Câu 2 : Hình bên là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
A \(\left( {0;1} \right)\) và \(\left( {2; + \infty } \right)\)
B \(\left( {1;2} \right)\)
C \(\left( {2; + \infty } \right)\)
D \(\left( {0;1} \right)\)
- Câu 3 : Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left( {-\infty ; + \infty } \right)\), có bảng biến thiên như hình sau:
A Hàm số nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)
B Hàm số đồng biến trên khoảng \(\left( {-\infty ;-2} \right)\)
C Hàm số nghịch biến trên khoảng \(\left( {-\infty ;1} \right)\)
D Hàm số đồng biến trên khoảng \(\left( {-1; + \infty } \right)\)
- Câu 4 : Tìm tập hợp các giá trị của m để hàm số \(y=\frac{x-m}{x+1}\) nghịch biến trên từng khoảng xác định là:
A \(\left( -\infty ;-1 \right)\).
B \(\left( -\infty ;1 \right]\).
C \(\left( -\infty ;-1 \right]\).
D \(\left( -1;+\infty \right)\).
- Câu 5 : Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số \(y = {x^3} - 3{x^2} + 1\)?
A Hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
B Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\)
C Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\)
D Hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right)\)
- Câu 6 : Cho hàm số \(y = \dfrac{{x + 3}}{{x + 2}}.\) Khẳng định nào sau đây đúng?
A Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 3} \right)\,\, \cup \,\,\left( { - 2; + \infty } \right).\)
B Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 2; + \infty } \right).\)
C Hàm số nghịch biến trên R.
D Hàm số ngịch biến trên \(R\backslash \left\{ 2 \right\}.\)
- Câu 7 : Hàm số \(y=\frac{{{x}^{4}}}{4}-2{{x}^{2}}+3\) nghịch biến trên khoảng nào?
A \(\left( -\infty ;-2 \right)\) và \(\left( 0;2 \right)\)
B \(\left( -2;0 \right)\)
C \(\left( 2;+\infty \right)\)
D \(\left( -2;0 \right)\) và \(\left( 2;+\infty \right)\)
- Câu 8 : Cho hàm số : \(y = {x^3} - 3{{\rm{x}}^2} - 3\). Mệnh đề nào dưới đây đúng
A Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\)
B Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\)
C Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
D Hàm số nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)
- Câu 9 : Cho hàm số \(y = \frac{{x - 2}}{{x - 1}}.\) Khẳng định nào sau đây là khẳng định đúng?
A Hàm số nghịch biến trên \(R\backslash \left\{ 1 \right\}.\)
B Hàm số đồng biến trên \(R\backslash \left\{ 1 \right\}.\)
C Hàm số đơn điệu trên R.
D Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\,\,1} \right)\) và \(\left( {1; + \infty } \right).\)
- Câu 10 : Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ dưới đây. Khẳng định nào sau đây là sai?
A
\(f\left( x \right)\) nghịch biến trên khoảng \(\left( -\infty ;-1 \right)\).
B \(f\left( x \right)\) đồng biến trên khoảng \(\left( 0;6 \right)\).
C \(f\left( x \right)\) nghịch biến trên khoảng \(\left( 3;+\infty \right)\).
D \(f\left( x \right)\) đồng biến trên khoảng \(\left( -1;3 \right)\).
- Câu 11 : Hàm số \(y={{x}^{3}}-3x+12\) đồng biến trên khoảng nào trong các khoảng sau đây?
A \(\left( 0;+\infty \right)\)
B \(\left( -\infty ;-1 \right)\)
C \(\left( -\infty ;1 \right)\)
D \(\left( -1;1 \right)\)
- Câu 12 : Cho hàm số \(y=\frac{2x+1}{1-x}\). Mệnh đề nào sau đây đúng ?
A Hàm số nghịch biến trên \(\left( -\infty ;1 \right)v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }\left( 1;+\infty \right)\).
B Hàm số đồng biến trên\(R\backslash \left\{ 1 \right\}\).
C Hàm số đồng biến trên \(\left( -\infty ;1 \right)v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }\left( 1;+\infty \right)\).
D Hàm số đồng biến trên \(\left( -\infty ;1 \right)\cup \left( 1;+\infty \right)\).
- Câu 13 : Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
A \(\left( -2;0 \right)\)
B \(\left( -\infty ;-2 \right)\)
C \(\left( 0;2 \right)\)
D \(\left( 0;+\infty \right)\)
- Câu 14 : Hàm số \(y={{x}^{3}}-3x\) nghịch biến trên khoảng nào?
A \(\left( -\infty ;-1 \right)\).
B \(\left( -\infty ;+\infty \right)\).
C \(\left( -1;1 \right)\).
D \(\left( 0;+\infty \right)\).
- Câu 15 : Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên sau. Tìm mệnh đề đúng?
A Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng \(\left( -2;\ 0 \right).\)
B Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng \(\left( -4;\ 0 \right).\)
C Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( -\infty ;\ 0 \right).\)
D Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( -4;\ +\infty \right).\)
- Câu 16 : Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
A \(\left( 1;+\infty \right)\).
B \(\left( 0;3 \right)\).
C \(\left( -\infty ;+\infty \right)\).
D \(\left( 2;+\infty \right)\).
- Câu 17 :
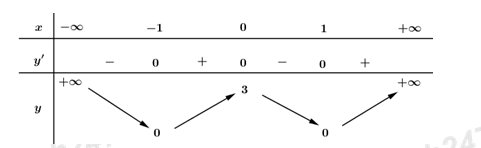Cho hàm số có bảng biến thiên như sau: A Hàm số đồng biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right)\).
B Hàm số nghịch biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right)\).
C Hàm số đồng biến trên các khoảng \(\left( 0;\ 3 \right)\) và \(\left( 0;+\infty \right).\)
D Hàm số đồng biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 0;1 \right).\)
- Câu 18 : Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên khoảng \(\left( a;b \right).\) Mệnh đề nào sau đây sai ?
A Nếu \({f}'\left( x \right)<0\) với mọi \(x\in \left( a;b \right)\) thì hàm số \(y=f\left( x \right)\) nghịch biến trên \(\left( a;b \right).\)
B Nếu \({f}'\left( x \right)>0\) với mọi \(x\in \left( a;b \right)\) thì hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( a;b \right).\)
C Nếu hàm số \(y=f\left( x \right)\) nghịch biến trên \(\left( a;b \right)\) thì \({f}'\left( x \right)\le 0\) với mọi \(x\in \left( a;b \right).\)
D Nếu hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( a;b \right)\) thì \({f}'\left( x \right)>0\) với mọi \(x\in \left( a;b \right).\)
- Câu 19 : Cho đồ thị hàm số như hình vẽ
A Hàm số nghịch biến trên \(\left( -\,\infty ;-\,1 \right).\)
B Hàm số luôn đồng biến trên \(\mathbb{R}.\)
C Hàm số đồng biến trên \(\left( -\,1;+\,\infty \right).\)
D Hàm số nghịch biến trên \(\left( 1;+\,\infty \right).\)
- Câu 20 : Cho hàm số phù hợp với bảng biến thiên sau
A Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;-\,\frac{1}{3} \right);\,\,\left( 1;+\,\infty \right)\) và đồng biến trên khoảng \(\left( -\frac{1}{3};1 \right).\)
B Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;2 \right)\cup \left( 3;+\,\infty \right)\) và đồng biến trên khoảng \(\left( 2;3 \right).\)
C Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;-\,\frac{1}{3} \right)\cup \left( 1;+\,\infty \right)\) và đồng biến trên khoảng \(\left( -\frac{1}{3};1 \right).\)
D Hàm số nghịch biến trên các khoảng \(\left( -\,\infty ;2 \right);\,\,\left( 3;+\,\infty \right)\) và đồng biến trên khoảng \(\left( 2;3 \right).\)
- Câu 21 : Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=\frac{x+{{m}^{2}}}{x+1}\) luôn đồng biến trên từng khoảng xác định.
A \(m\in \left[ -\,1;1 \right].\)
B \(m\in \mathbb{R}.\)
C \(m\in (-1;1).\)
D \(m\in \left( -\,\infty ;-\,1 \right)\cup \left( 1;+\,\infty \right).\)
- Câu 22 : Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên:
A 4
B 2
C 1
D 3
- Câu 23 : Hàm số \(y=f\left( x \right)\) có đạo hàm \(y'={{x}^{2}}\). Mệnh đề nào dưới đây đúng?
A Hàm số đồng biến trên \(\left( -\infty ;0 \right)\) và nghịch biến trên \(\left( 0;+\infty \right)\).
B Hàm số đồng biến trên R.
C Hàm số nghịch biến trên R.
D Hàm số nghịch biến trên \(\left( -\infty ;0 \right)\) và đồng biến trên \(\left( 0;+\infty \right)\).
- Câu 24 : Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ bên.
A Nghịch biến trên khoảng \((-3;\,\,0).\)
B Đồng biến trên khoảng \((0;\,\,2).\)
C Đồng biến trên khoảng \((-1;\,\,0).\)
D Nghịch biến trên khoảng \((0;\,\,3).\)
- Câu 25 : Đường cong trong hình vẽ bên là đồ thị của hàm số có dạng \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\,\left( a\ne 0 \right).\) Hàm số đồng biến trên khoảng nào dưới đây ?
A
\(\left( 1;+\,\infty \right).\)
B
\(\left( -\,1;+\,\infty \right).\)
C
\(\left( -\,\infty ;1 \right).\)
D
\(\left( -\,1;1 \right).\)
- Câu 26 : Cho hàm số \(y=f\left( x \right)\) thỏa mãn \({f}'\left( x \right)={{x}^{2}}-5x+4.\) Khẳng định nào sau đây là đúng ?
A Hàm số đã cho đồng biến trên khoảng \(\left( -\,\infty ;3 \right).\)
B Hàm số đã cho nghịch biến trên khoảng \(\left( 3;+\,\infty \right).\)
C Hàm số đã cho nghịch biến trên khoảng \(\left( 2;3 \right).\)
D Hàm số đã cho đồng biến trên khoảng \(\left( 1;4 \right).\)
- Câu 27 : Cho hàm số \(f\left( x \right)\) liên trục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào ?
A \(\left( -\,\infty ;0 \right).\)
B \(\left( -\,\infty ;-\,1 \right).\)
C \(\left( 1;+\,\infty \right).\)
D \(\left( -\,1;1 \right).\)
- Câu 28 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
A \(\left( { - 2; + \infty } \right)\)
B \(\left( {1; + \infty } \right)\)
C \(\left( { - 2;3} \right)\)
D \(\left( { - \infty ; - 1} \right)\)
- - Trắc nghiệm Toán 12 Chương 2 Bài 1 Lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 2 Hàm số lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 4 Hàm số mũ và hàm số lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 5 Phương trình mũ và phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 6 Bất phương trình mũ và bất phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 3 Bài 1 Nguyên hàm
- - Trắc nghiệm Toán 12 Chương 3 Bài 2 Tích phân
- - Trắc nghiệm Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học
- - Trắc nghiệm Toán 12 Bài 1 Số phức
- - Trắc nghiệm Toán 12 Bài 2 Cộng, trừ và nhân số phức
Liên kết với Facebook
Liên kết với Google