Tổng hợp phương pháp tìm giá trị lớn nhất, nhỏ nhất của hàm số cần nắm rõ

CÁCH TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ 

Bộ môn Toán Giải tích lớp 12 các em học sinh sẽ được học dạng bài tập: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Cunghocvui.com sẽ tổng hợp phương pháp dạng bài tập này. 

I. Định nghĩa GTLN, GTNN của hàm số

Cho hàm số \(y =\) \(f(x)\) xác định trên tập D. 

- M là GTLN của \(y = f(x)\) trên tập D khi: \(\left\{\begin{matrix}f(x) \leqslant M & \\ \exists x_{o, f(x_{o}) = M} & \end{matrix}\right.\)

- m là GTNN của \(y = f(x)\) trên tập D khi: \(\left\{\begin{matrix}m \leqslant f(x),\forall x_{o} \in D & \\ \forall x_{o} \in D, f(x_{o}) = m & \end{matrix}\right.\)

II. Cách tìm GTLN, GTNN của hàm số

1. Tìm GTLN, GTNN của hàm số trên một đoạn

Định lý: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất, nhỏ nhất trên đoạn đó. 

Quy tắc: Tìm GTLN, GTNN của hàm số \(f(x)\) liên tục trên một đoạn \(\begin{bmatrix}a; b\end{bmatrix}\).

- Tìm các điểm \(x_{i} \in (a; b)\) (i = 1, 2,...,n) mà tại đó \(f'(x_{i}) = 0 \) hoặc \(f'(x_{i}) \) không xác định.

- Tính \(f(x)\) , \(f(b)\), \(f(x_{i}) \) (i = 1, 2,...,n).

GTLN, GTNN trong các giá trị trên là GTLN, GTNN của hàm số \(f\) trên \(\begin{bmatrix}a, b\end{bmatrix}\).

2. Tìm GTLN, GTNN của hàm số trên một khoảng

Để tìm GTLN, GTNN của hàm số  \(y = f(x)\) xác định trên tập D, tiến hành khảo sát sự biến thiên của hàm số trên D, sau đó căn cứ bảng biến thiên của hàm số và kết luận GTLN, GTNN của hàm số. 

Quy tắc: Tìm GTLN, GTNN của hàm số \(y = f(x)\) trên khoảng \((a, b)\) .

- Tính \(f'(x)\). Tìm các điểm mà tại đó \(f'(x)\) = 0 hoặc \(f'(x)\) không xác định. 

- Lập bảng biến thiên. 

- Dựa vào bảng biến thiên kết luận GTLN, GTNN. 

3. Tìm GTLN, GTNN của hàm số chứa tham số m 

Hàm số có chứa tham số m và thỏa mãn điều kiện về GTLN, GTNN trên một đoạn. 

Ví dụ:

Ví dụ cách tìm GTLN, GTNN của hàm số chứa tham số m

III. Cách tìm GTLN, GTNN của hàm số bằng máy tính 

1. Tìm GTLN, GTNN của hàm số trên một đoạn

Tìm GTLN, GTNN của hàm số \(f(x)\) liên tục trên một đoạn \(\begin{bmatrix}a; b\end{bmatrix}\).

Các bước thực hiện:

- Bước 1: Dùng lệnh MODE 7 để lập bảng giá trị trên máy tính Casio.

- Bước 2: Nhập f(x) = ...

Start?a= \(\rightarrow \) End?b= \(\rightarrow \) Step? \(\alpha \) = ?

(\(\alpha \) chọn tùy thuộc vào đề bài)

Ta nhận được bảng giá trị, quan sát sẽ thấy GTLN hiển thị là max, GTNN hiển thị là min. 

Nếu đề bài liên quan đến lượng giác như sinx, cosx...chuyển máy tính sang chế độ radian bằng lệnh SHIEF MODE 4 và tính. 

Ví dụ: Tìm GTLN, GTNN của hàm số \(y = x^{3} + 3x^{2} \) trên đoạn \(\begin{bmatrix}-1, 3\end{bmatrix}\).

Nhập MODE 7, nhập \(f(x) = x^3 + 3x^2\), Start?-1 = End? 3 = Step? 0.5 = 

Ta được bảng giá trị và ta thấy f(3) = 54 là GTLN, f(0) = 0 là GTNN. 

2. Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một khoảng 

Các bước tương tự như dạng 1 nhưng cần chú ý đề để chọn GTLN, GTNN. Cần xem kỹ x có thuộc miền trong đề bài không. 

3. Tìm GTLN, GTNN của hàm số chứa tham số m 

Ví dụ: 

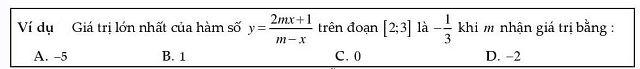
Ví dụ sử dụng máy tính tìm giá trị lớn nhất, nhỏ nhất có chứa tham số m 

Trên đây là toàn bộ phương pháp tìm giá trị lớn nhất, nhỏ nhất của hàm số, rất mong giúp được quý độc giả. Sau khi học xong lý thuyết, các em có thể tham khảo thêm bài tập tìm GTLN, GTNN của hàm số.