Mẹo toán học chuẩn nhất về tâm đường tròn ngoại tiếp tam giác

Những mẹo toán học nhanh về đường tròn ngoại tiếp như cách vẽ đường tròn ngoại tiếp, tâm đường tròn ngoại tiếp tam giác vuông, cách xác định tâm đường tròn ngoại tiếp tứ giác đều được Cunghocvui tổng hợp đầy đủ ở bài viết này.

I) Đường tròn ngoại tiếp tam giác

1) Khái niệm

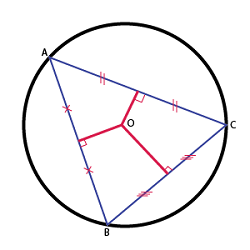
Đường tròn ngoại tiếp tam giác là đường tròn thỏa mãn điều kiện đi qua cả ba đỉnh của tam giác. Cách nói khác của đường tròn ngoại tiếp là tam giác nội tiếp đường tròn.

2) Cách xác định tâm đường tròn ngoại tiếp tam giác (hay cách vẽ đường tròn ngoại tiếp)

Để có thể xác định tâm đường tròn ngoại tiếp tam giác nói chung và tâm đường tròn ngoại tiếp tam giác nói riêng thì chúng ta cần phải ghi nhớ lý thuyết.

Tâm đường tròn ngoại tiếp tam giác thường sẽ là giao điểm 3 đường trung trực, hoặc cũng có thể chỉ là giao điểm 2 đường trung trực.

3) Mở rộng cách xác định tâm đường tròn ngoại tiếp tứ giác đã nội tiếp

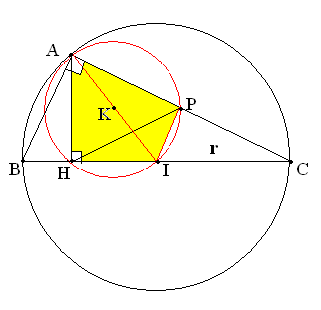
Ta xác định tương tự như trong tam giác, dựa vào tính chất nằm trên đường trung trực của một đoạn thẳng cách đều 2 đỉnh tứ giác. 

Tâm đường tròn ngoại tiếp tứ giác nằm trền các đường trung trực.

II) Tính bán kính đường tròn ngoại tiếp tam giác

Gọi a, b, c lần lượt là độ dài các cạnh BC, AC, AB của tam giác ABC.

- Nửa chu vi tam giác

\(p=\dfrac {a+b+c}{2}\)

- Diện tích tam giác

\(S = \sqrt{p(p-a).(p-b)(p-c)}\)'

- Bán kính đường tròn ngoại tiếp

\(R = \dfrac {a.b.c}{4S}\)

• Góc A

\(r_a = \dfrac {2S}{b+c-a}=\dfrac {S} {p-a} = p.tan\dfrac{A}{2}\)

• Góc B

\(r_b = \dfrac {2S}{c+a-b}=\dfrac {S} {p-b} = p.tan\dfrac{B}{2}\)

• Góc C

\(r_c = \dfrac {2S}{a+b-c}=\dfrac {S} {p-c} = p.tan\dfrac{C}{2}\)

III) Luyện tập

Bài 1: Cho biết độ dài ba cạnh \(\Delta ABC\) lần lượt là: AB = 3cm; AC = 7cm; BC = 8cm. Hãy tính \(S_{ABC}\) và \(r_{ngtABC}\)

Hướng dẫn:

- \(S_{ABC} = 6\sqrt{3}\)

- Để tính được đường tròn ngoại tiếp tam giác thì ta cần tính p: \(p = 9\). Suy ra: \(R = \dfrac {7\sqrt{3}}{3}\)

Bài 2: Cho tam giác ABC cân ở A. Các đường cao AG, BE, CF cắt nhau tại H. Hãy xác định tâm của đường tròn ngoại tiếp tứ giác AEHF và chứng minh GE là tiếp tuyến của đường tròn tâm \(I\)

Trên đây là bài viết mà Cunghocvui đã tổng hợp đường về tâm đường tròn ngoại tiếp tam giác, hy vọng bài viết sẽ giúp ích cho các bạn trong quá trình học tập. Hãy để lại comment câu trả lời và ý kiến thắc mắc ở phưới dưới nhé!