Giải bài 61 trang 91 - Sách giáo khoa Toán 9 tập 2
Đề bài
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
Hướng dẫn giải
a) Vẽ đường tròn (O;2)
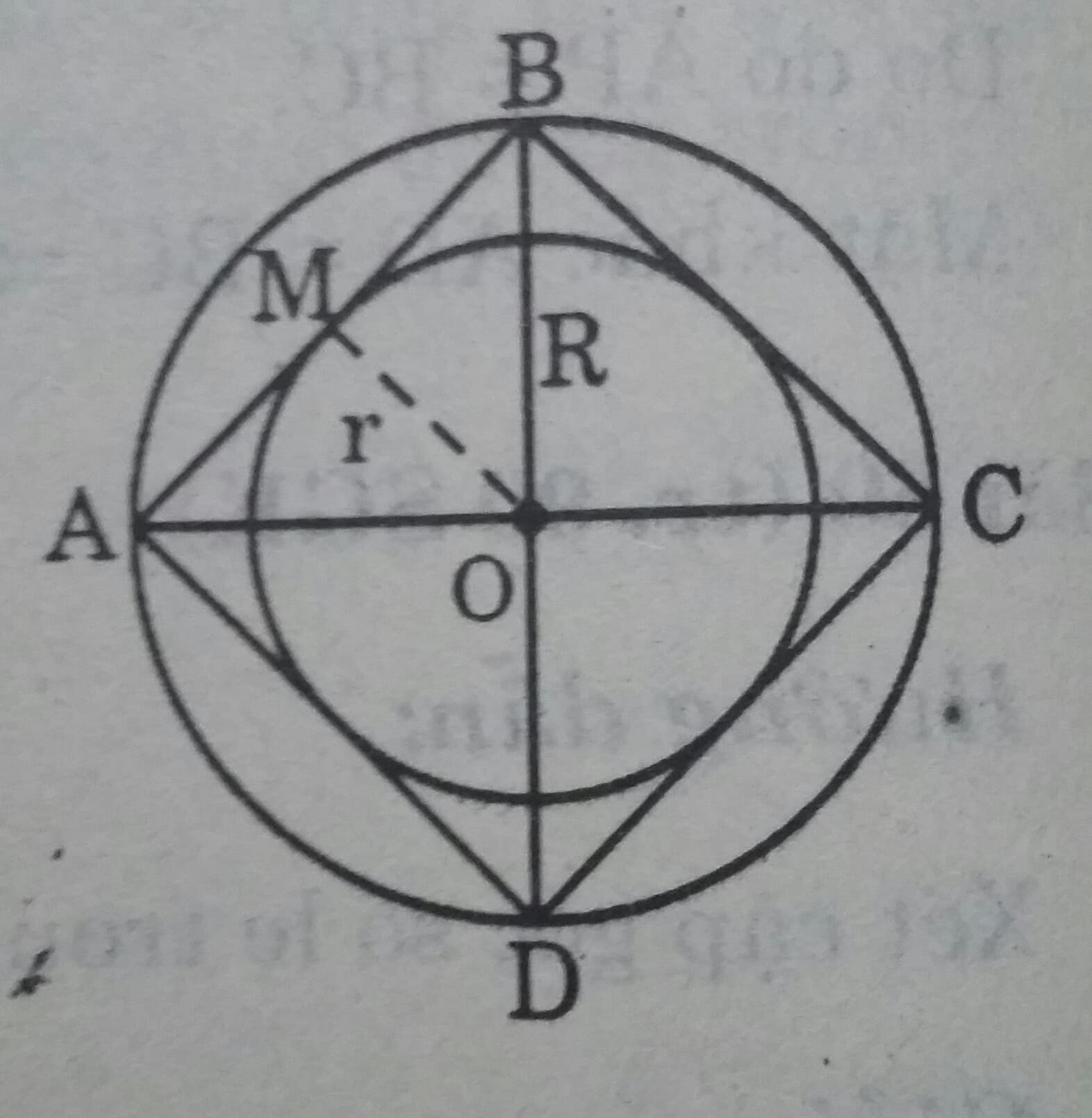
b) Vẽ hai đường kính AC và BD vuông góc với nhau.
Vẽ các dây AB, BC , CD, DA ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ \( OM \perp AB \)
OM là đường kính r của đường tròn nội tiếp hình vuông ABCD.
Vì \(OM = - \dfrac{1}{2}BC= - \dfrac{1}{2}BC= -\dfrac{1}{2}AB= MB \ nên \ \\ \ Delta MOB \ vuông \ cân \ , ta \ có:\\ r^2 + r^2 = OB^2 .\\ \Rightarrow 2r^2 = 2^2 \Rightarrow r = \sqrt{2}(cm)\)
Vẽ đường tròn (O; \( \sqrt{2}\) cm) ta được đường tròn nội tiếp hình vuông ABCD.