Giải bài 70 trang 141 - Sách giáo khoa Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh rằng tam giác AMN là tam giác cân

b) Kẻ BH ⊥ AM, kẻ CK ⊥ AN. Chứng minh rằng BH = CK

c) CMR AH = AK

d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? Vì sao

e) Khi góc BAC = 60o và BM = CN = BC hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC

Hướng dẫn giải

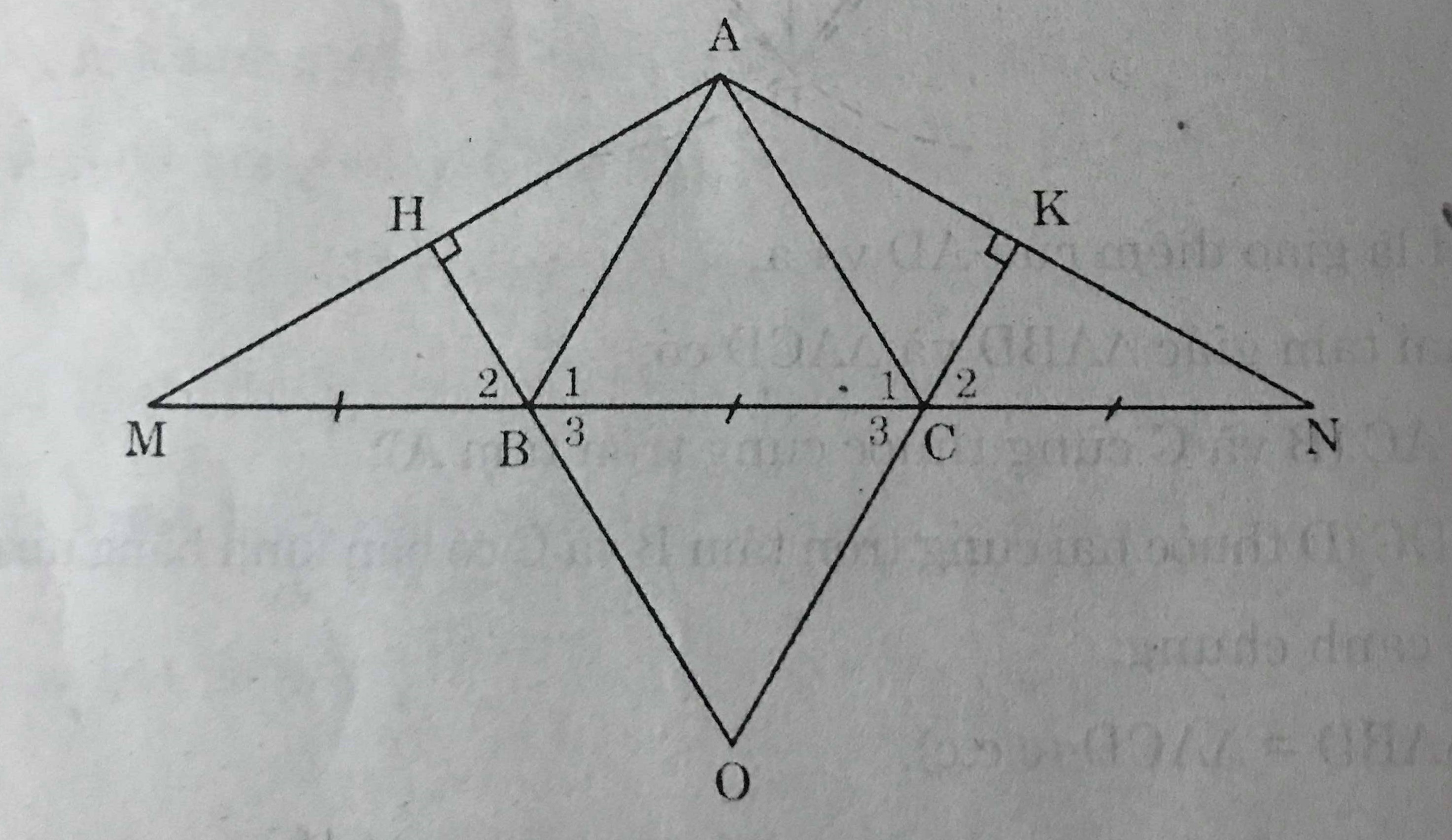
a) ΔABC cân tại A => \(\widehat{B_1}=\widehat{C_1}\) (hai góc ở đáy của tam giác cân)

=> \(\widehat{ABM}=\widehat{ACN}\) (cùng bù hai góc bằng nhau)

ΔABM và ΔACN có :

AB = AC (hai cạnh của tam giác cân ABC)

\(\widehat{ABM}=\widehat{ACN}\)

BM = CN (giả thiết)

Nên ΔABM = ΔCAN (c.g.c)

Suy ra : \(\widehat{M}=\widehat{N}\) => ΔAMN là tam giác cân

b) ΔAHM và ΔCKN có :

\(\widehat{MHB}=\widehat{NKC}=90^0\) ( \(BH \bot AM, CK \bot AN\) )

BM = CN (giả thiết)

\(\widehat{M}=\widehat{N}\) (câu a)

Nên ΔAHM = ΔCKN (cạnh huyền - góc nhọn)

Suy ra : BH = CK

c) ΔABH và ΔACK có :

\(\widehat{H}=\widehat{K}=90^0\) (giả thiết)

BH = CK (câu a)

AB = AC (hai cạnh bên của tam giác cân ABC)

Nên ΔABH = ΔACK (cạnh huyền - cạnh góc vuông)

Suy ra : AH = AK

d) Theo câu b) ΔBHM = ΔCKN

=> \(\widehat{B_2}=\widehat{C_2}\) (hai góc tương ứng của hai tam giác bằng nhau)

=> \(\widehat{B_3}=\widehat{C_3}\) (hai góc đối đỉnh của hai góc bằng nhau)

=>  ΔOBC là tam giác cân

e) ΔABC cân nên ta có \(\widehat{BAC}\) = \(60^0\) nên là tam giác đều:

=> \(\widehat{B_1}=\widehat{C_1}=60^0\)

ΔABM có AB = BM (cùng bằng BC) nên là tam giác cân

Mà \(\widehat{ABM}= 180^0 - \widehat{B_1}=120^0\)

Nên \(\widehat{M}=\dfrac{180^0-120^0}{2}=30^0\)

Tương tự \(\widehat{N}=30^0\)

Vậy ΔAMN có \(\widehat{M}=\widehat{N}=30^0\) , \(\widehat{MAN}=120^0\)

ΔMHB vuông có \(\widehat{M}=30^0\) nên \(\widehat{B_2}=60^0\)

Suy ra : \(\widehat{B_3}=60^0\) (hai góc đối đỉnh)

Vậy ΔAMN là tam giác đều