Bài 7 trang 114 SGK Hình học 11

Đề bài

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = a, BC = b, CC' = c$.

a) Chứng minh rằng mặt phẳng $(ADC'B')$ vuông góc với mặt phẳng $(ABB'A')$.

b) Tính độ dài đường chéo $AC'$ theo $a, b, c$.

Hướng dẫn giải

a) Chứng minh $DA \bot \left( {ABB'A'} \right)$

b) Sử dụng định lí Pytago.

Lời giải chi tiết

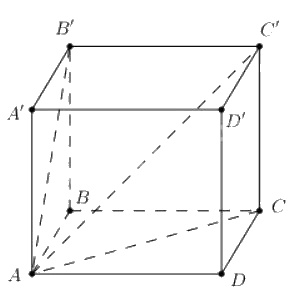
a) Ta có: $DA ⊥ (ABB'A'), DA ⊂ (ADC'B')$

$\Rightarrow (ADC'B') \bot(ABB'A')$.

b) Xét tam giác vuông $ACC'$) 

 $AC' = \sqrt {A{C^2} + CC{'^2}}  = \sqrt {A{D^2} + D{C^2} + CC{'^2}}$

          $=\sqrt{a^{2}+b^{2}+c^{2}}.$

Ghi nhớ: Hai mặt phẳng vuông góc với nhau khi mặt này chứa một đường thẳng vuông góc với mặt kia.