Bài 11 trang 114 SGK Hình học 11

Đề bài

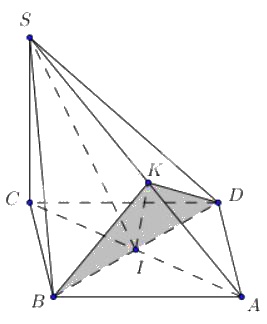
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình thoi tâm \(I\) cạnh \(a\) và có góc \(A\) bằng \(60^{0},\) cạnh \(SC=\frac{a\sqrt{6}}{2}\) và \(SC\) vuông góc với mặt phẳng \((ABCD)\).

a) Chứng minh mặt phẳng \((SBD)\) vuông góc với mặt phẳng \((SAC)\). 

b) Trong tam giác \(SCA\) kẻ \(IK\) vuông góc với \(SA\) tại \(K\). Hãy tính độ dài \(IK\)

c) Chứng minh \(\widehat{BKD}=90^{0}\) và từ đó suy ra mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SAD)\).

Hướng dẫn giải

a) Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

b) Chứng minh tam giác \(SCA\) và \(IKA\) đồng dạng, từ đó suy ra tỉ số các cạnh và tính \(IK\).

c) Chứng minh tam giác \(BKD\) có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy.

Xác định góc giữa hai mặt phẳng \((SAB)\) và \((SAD)\) và chứng minh góc đó bằng \(90^0\).

Lời giải chi tiết

a) \(SC \bot \left( {ABCD} \right) \Rightarrow SC \bot BD\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

\(ABCD\) là hình thoi nên \(AC\bot BD\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(BD ⊥ (SAC)\).

Mà \(BD\subset (SBD)\Rightarrow (SBD) ⊥ (SAC)\).

b) Xét tam giác vuông \(ABI\) có: \(AI=AB.\cos 30^0={{a\sqrt 3 } \over 2}\Rightarrow AC = 2AI = a\sqrt 3 \)

 Xét tam giác vuông \(SAC\) có: \(SA=\sqrt {A{C^2} + S{C^2}}  = \sqrt {3{a^2} + {{6{a^2}} \over 4}} =\frac{3a}{\sqrt{2}}.\) 

Dễ dàng chứng minh đươc \(\Delta SCA \sim \Delta IKA\,\,\left( {g.g} \right)\)

\(\Rightarrow \frac{IK}{SC}=\frac{AI}{AS}\Rightarrow IK=\frac{AI.SC}{AS}=\frac{a}{2}.\)

c) Dễ thấy \(\Delta ABD\) đều nên \(BD = a \Rightarrow IK = \frac{1}{2}BD\) nên \(\Delta BKD\) vuông tại \(K\). Vậy \(\widehat{BKD}=90^{0}.\)

Ta có: \(BD \bot \left( {SAC} \right)\,\,\left( {cmt} \right) \Rightarrow BD \bot SA\)

\(\left\{ \begin{array}{l}BD \bot SA\\IK \bot SA\end{array} \right. \Rightarrow SA \bot \left( {BKD} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot BK\\SA \bot DK\end{array} \right.\)

Ta có: 

\(\begin{array}{l}
\left\{ \begin{array}{l}
BD \bot SA\\
IK \bot SA
\end{array} \right. \Rightarrow SA \bot \left( {BKD} \right) \\ \Rightarrow \left\{ \begin{array}{l}
\left( {SAB} \right) \cap \left( {SAD} \right) = SA\\
\left( {SAB} \right) \supset BK \bot SA\\
\left( {SAD} \right) \supset DK \bot SA
\end{array} \right.\\
\Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SAD} \right)} \right)} = \widehat {\left( {BK;DK} \right)} = \widehat {BKD} = {90^0}\\
\Rightarrow \left( {SAB} \right) \bot \left( {SAD} \right)
\end{array}\)