Bài 4 trang 8 SGK Hình học 11

Đề bài

Cho hai đường thẳng $a$ và$b$ song song với nhau. Hãy chỉ ra một phép tịnh tiến biến $a$ thành $b$. Có bao nhiêu phép tịnh tiến như thế?

Hướng dẫn giải

Tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu.

Lời giải chi tiết

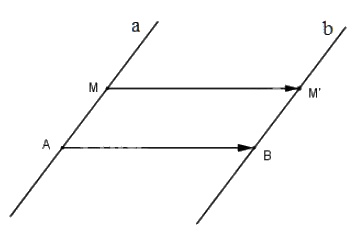
Giả sử $a$ và $b$ có vectơ chỉ phương là $\overrightarrow{v}$

. Lấy điểm $A$ bất kì thuộc $a$ và điểm $B$ bất kì thuộc $b$. Với mỗi điểm $M$, gọi $M'$ = $T_{\vec{AB}}$ $(M)$ . Khi đó $\overrightarrow{MM'}$= $\overrightarrow{AB}$. Suy ra $\overrightarrow{AM}$ = $\overrightarrow{BM'}$

Ta có:

$M ∈ a ⇔$ $\overrightarrow{AM}$ cùng phương với $\overrightarrow{v}$ ⇔ $\overrightarrow{BM'}$  cùng phương với $\overrightarrow{v}$ $⇔ M' ∈  b$.

Từ đó suy ra phép tịnh tiến theo $\overrightarrow{AB}$ biến $a$ thành $b$.

Vì $A,B$ là các điểm bất kì  ( trên $a$ và $b$ tương ứng) nên có vô số phép tịnh tiến biến $a$ thành $b$.