Bài 13 trang 74 SGK Toán 8 tập 1

Đề bài

Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.

Hướng dẫn giải

- Áp dụng: tính chất hình thang cân, tính chất hai tam giác bằng nhau, tính chất tam giác cân.

Lời giải chi tiết

Do ABCD là hình thang cân (gt) nên AD = BC, AC = BD, \(\widehat{ADC}=\widehat{BCD}\) (tính chất hình thang cân)

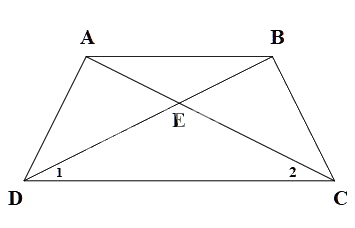
Xét \(\Delta A{\rm{D}}C\) và \(\Delta B{\rm{C}}D\)

         AD = BC (cmt)

         AC = BD (cmt)

         DC chung

Nên  ∆ADC =  ∆BCD (c.c.c)

Suy ra \(\widehat{C_{2}}=\widehat{D_{1}}\) (2 góc tương ứng)

Do đó \(\Delta E{\rm{D}}C\) cân tại E (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow EC = E{\rm{D}}\) (tính chất tam giác cân)

Lại có:\(\left\{ \begin{array}{l}
AC = B{\rm{D}}\left( {cmt} \right)\\
EC = E{\rm{D}}\left( {cmt} \right)\\
E{\rm{A}} = AC - CE\left( {gt} \right)\\
EB = B{\rm{D}} - DE\left( {gt} \right)
\end{array} \right. \Rightarrow E{\rm{A}} = EB\).