Bài 1 trang 45 SGK Hình học 10

Đề bài

Cho tam giác vuông cân \(ABC\) có \(AB = AC = a\). Tính các tích vô hướng \(\vec{AB}.\vec{AC}\), \(\vec{AC}.\vec{CB}\).

Hướng dẫn giải

Cho hai vecto \(\overrightarrow a\) và \( \overrightarrow b \) đều khác vecto \( \overrightarrow 0. \) Khi đó tích vô hướng của vecto \(\overrightarrow a\) và \( \overrightarrow b \) được xác định bởi công thức sau:

\[\overrightarrow a \overrightarrow {.b}  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\]

Lời giải chi tiết

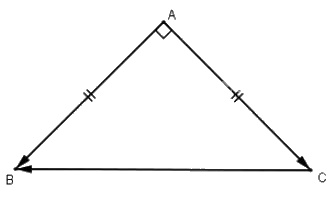
\(\vec{AB} ⊥\vec{AC}\Rightarrow \vec{AB}.\vec{AC}  = 0\)

\(\vec{AC}.\vec{CB} =- \vec{CA}\). \(\vec{CB}\)

Ta có: \(CB= \sqrt{AB^2+AC^2}\)\(=\sqrt{a^2+a^2}=a\sqrt2\);  \(\widehat{C} = 45^0\) vì \(\Delta ABC\) là tam giác vuông cân tại \(A.\) 

Vậy   \(\vec{AC}.\vec{CB} = -\vec{CA}. \vec{CB}\)\(= -|\vec{CA}|. |\vec{CB}|. cos45^0\)

\(= - a.a\sqrt 2 .{{\sqrt 2 } \over 2} =  - {a^2}.\)