Tìm hiểu về định nghĩa và tính chất của đường trung tuyến

Tìm hiểu về định nghĩa và tính chất của đường trung tuyến

Bài viết hôm nay sẽ đem lại cho bạn khái niệm đường trung tuyến là gì? Tính chất của đường thẳng đó trong tam giác thường gồm những tính chất nào? Bạn có đang tò mò không, nếu có hãy tham khảo ngay bài viết dưới đây nhé!

I. Định nghĩa về đường trung tuyến

    1. Đường trung tuyến là gì?

Đường trung tuyến được định nghĩa là đường thẳng nối từ đỉnh đến trung điểm của cạnh đối diện trong một tam giác. Chính vì vậy, có ba đường TT trong một tam giác. Đối với các tam giác đặc biệt như tam giác cân và đều, mỗi đường TT sẽ phân góc ở định thành 2 góc bằng nhau, với điều kiện hai cạnh bên phải có độ dài bằng nhau.

Giao điểm của ba đường TT trong tam giác gọi là trọng tâm.

Công thức liên quan:

• Bài 4. Phép thử và biến cố

• Bài 5. Xác suất và biến cố

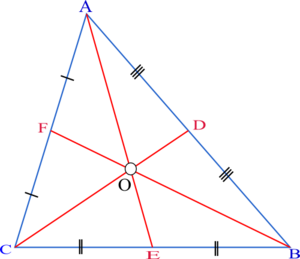
    2. Cách xác định đường trung tuyến trong tam giác

Để xác định đường TT của một tam giác ta thực hiện:

• Tìm trung điểm E của BC sao cho EC = EB
• Nối A với E ta được đường TT AE.
• Tương tự với các đường TT còn lại.
• Gia 3 đường TT là điểm O. Suy ra O chính là trọng tâm tam giác ABC.

II. Tính chất đường trung tuyến trong tam giác thường

Cho tam giác ABC có AM, BN, CP lần lượt là ba đường TT tại đỉnh A, B, C. Ta có giao của ba đường TT là điểm G. Vậy G là trọng tâm của tam giác ABC.

Ta có tính chất:

\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM} \Rightarrow AG=\dfrac{2}{3} AM\)

\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

Các công thức tính đường TT:

\(\begin{array}{l} {m_a} = \sqrt {\frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4}} \\ {m_b} = \sqrt {\frac{{{a^2} + {c^2}}}{2} – \frac{{{b^2}}}{4}} \\ {m_c} = \sqrt {\frac{{{b^2} + {a^2}}}{2} – \frac{{{c^2}}}{4}} \end{array}\)

Các hệ quả:

• Đường TT ứng với cạnh góc vuông sẽ bằng nửa cạnh huyền và ngược lại tam giác mà có đường TT bằng nửa cạnh huyền thì đó là tam giác vuông.
• Đường trung tuyến trong tam giác đều đồng thời là đường phân giác là đường cao và đường trung trực của tam giác đó.

III. Bài tập

Bài 1: Cho đề bài như sau:

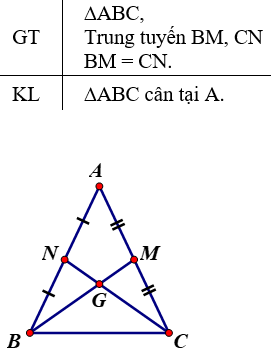
Lời giải:

Vì BM và CN là hai đường TT của tam giác mà BM giao CN tại G, nên ta có:

\(\dfrac{BG}{BM}=\dfrac{CG}{CN}=\dfrac{2}{3}\)

Mà BM = CN nên BG = CN và GN = GM

Xét \(\Delta BNG \ và \ \Delta CGM\) ta có:

BG = CN

GN = GM

\(\widehat{BGN}= \widehat{CGM}\) ( 2 goc đối đỉnh)

Suy ra : \(\Delta BNG \ đồng \ dạng \ \Delta CMG\)

Suy ra: BN = CM (1)

mà M và N lần lượt là trung điểm của AB và AC (2)

Từ (1) và (2) ta cí AB = AC => Tam giác ABC cân tại A( đpcm).

Bài 2: Đẳng thức nào dưới đây là đúng?

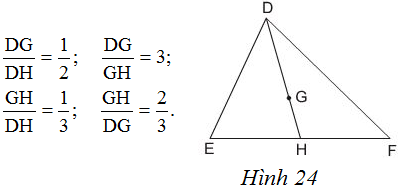
Lời giải:

Luyện tập thêm tại: Bài 4. Tính chất ba đường trung tuyến của tam giác

Qua bài viết trên bạn đã có câu trả lời cho bản thân mình chưa. Chúng tôi còn có rất nhiều bài viết hay đang chờ đón bạn, hãy cập nhật thường xuyên nhé!