Lý thuyết đường kính và dây của đường tròn chi tiết nhất

Đường kính và dây của đường tròn là một trong những kiến thức cơ bản của chương II hình học  Toán 9 nghiên cứu về Đường tròn. Cùng Cunghocvui tìm hiểu về lý thuyết và các bài tập về đường kính và dây của đường tròn qua bài viết này. Hy vọng nó hữu ích với các bạn!

A. Các lý thuyết cần nhớ về đường kính và dây của đường tròn

1. So sánh độ dài của đường kính và độ dài của dây 

Xét về yếu tố độ dài của các dây trong đường tròn, đường kính là một dây đặc biệt, đi qua tâm đường tròn và có độ dài lớn nhất.

2. Xét yếu tố vuông góc giữa các dây và đường kính. 

- Xét trong phạm vi một đường tròn, nếu đường kính tạo với dây một góc có độ lớn bằng $90^0$ thì trung điểm của dây đó thuộc đường kính hay nói cách khác là đường kính qua trung điểm của dây. 

- Xét trong phạm vi một đường tròn, nếu trung điểm của một dây cung (dây cung không đi qua tâm đường tròn) mà thuộc đường kính thì dây cung đó tạo với đường kính một góc có độ lớn bằng $90^0$

3. Mối tương quan giữa dây cung và độ dài khoảng cách từ dây cung đến tâm

Các tính chất về hai dây cung trong phạm vi một đường tròn như sau:

- Nếu hai dây cung có độ dài khoảng cách giữa hai đầu mút bằng nhau thì khoảng cách từ hai dây cung đó đến đường tròn là bằng nhau. Điều này cũng đúng trong trường hợp ngược lại, có nghĩa là nếu khoảng cách từ hai dây cung đến đường tròn là bằng nhau thì độ dài hai dây cung đó là bằng nhau.

- Nếu độ dài của dây cung nào lớn hơn thì khoảng cách từ dây cung đó đến tâm nhỏ hơn hay nói cách khác là tâm gần dây cung đó hơn. Điều này cũng đúng trong trường hợp ngược lại, có nghĩa là nếu tâm đường tròn gần dây cung nào hơn thì dây đó có độ dài lớn hơn.

B. Giải toán bài đường kính và dây của đường tròn

Dạng 1: So sánh hoặc chứng minh hai dây cung bằng nhau, lớn hơn, nhỏ hơn.

a, Các phương pháp so sánh hoặc chứng minh

- Dùng các tính chất về hai dây cung trong phạm vi một đường tròn theo mục 2

- Sử dụng các phương pháp chứng minh hai tam giác, mối tương quan giữa các yếu tố trong tam giác.

b, Một số bài tập áp dụng 

Bài 1: Cho một đường tròn, O là tâm đường tròn, một đường kính với hai đầu A và B với một dây cung $CD$ không giao với đường kính $AB$. Từ điểm A kẻ $AH$ sao cho đoạn thẳng $AH$ tạo với đoạn thẳng $CD$ một góc có độ lớn bằng $90^0$ (H thuộc $CD$ kéo dài) và tương tự với đoạn thẳng $BK$ xuất phát từ điểm B (K thuộc $CD$ kéo dài). Hãy sáng tỏ $CH=DK$?

Hướng dẫn giải bài tập

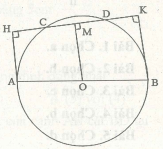
Xuất phát từ trung điểm O của đường tròn, kẻ $OM\perp CD$ ($CD$ nhận M làm trung điểm) => $OM//AH//BK$ (cùng tạo với $CD$ một góc bằng $90^0$)

Trong hình thang $AHKB$ có $OM//AH$ và $OA=OB$

=> Hình thang $AHKB$ nhận $OM$ là đường trung bình => $MH=MK$

Vì $OM\perp CD$ nên $MC=MD$

Ta có: $CH$ = $HM-CM$

          $DK$ = $MK-MD$

=> $CH=DK$

Bài 2: Cho một đường tròn, O là tâm đường tròn, một đường kính với hai đầu A và B với một dây cung $CD$ giao cắt với đường kính $AB$ tại điểm M ($CD$ nhận M làm trung điểm). Hãy làm sáng tỏ rằng tam giác $BCD$ là một tam giác đều.

Hướng dẫn giải bài tập: 

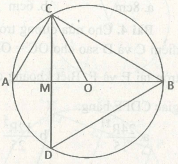
Vì $CD$ nhận M làm trung điểm nên $CM\perp AB$ 

=> $CM$ có hai chức năng, vừa là trung tuyến vừa là đường cao của tam giác $ACO$ 

=> $\Delta ACO$ là một tam giác cân tại đỉnh C (1)

Mặt khác, cũng xét trong tam giác $ACO$ có $OC=OA=R$ (vì hai điểm A và C cùng thuộc đường tròn) 

=> $\Delta ACO$ là một tam giác cân tại đỉnh O (2)

Từ (1) và (2) => $\Delta ACO$ là một tam giác đều (vì có hai góc $\widehat{ACO}$ và $\widehat{AOC}$ bằng nhau).

Theo dữ kiện đề bài ta có: Vì điểm C thuộc đường tròn tâm O nên $\widehat{ACB} = 90^0$ (góc chắn nửa đường tròn)

Mà $\widehat{ACD} =\widehat{ACO}+\widehat{OCD}$ => $\widehat{OCD}$ = $\widehat{ACD} -\widehat{ACO}$ = $90^0-60^0=30^0$

=> $\widehat{CBD}=60^0$ (vì $\widehat{CBD}$ nhận $AB$ là tia phân giác)

Tương tự với góc $\widehat{ABD} = 30^0$

Xét trong phạm vi của tam giác $CBD$ có $BM$ vừa nhận chức năng là đường phân giác, vừa nhận chức năng là đường cao hạ từ đỉnh B 

=> $\Delta {BCD}$ là một tam giác cân tại đỉnh B 

Kết hợp hai điều kiện là $\Delta {BCD}$ là một tam giác cân tại đỉnh B và $\widehat{CBD}=60^0$

=> $\Delta {BCD}$ là tam giác đều (điều phải chứng minh).

Dạng 2: Xác định độ lớn của đoạn thẳng và các yếu tố khác

a, Phương pháp xác định độ lớn và các yếu tố

- Sử dụng tính chất quan hệ giữa đường kính và các dây cung trong phạm vi một đường tròn.

- Sử dụng các công thức của hệ thức lương, định lý Py-ta-go dùng trong tam giác vuông.

b, Một số bài tập áp dụng

Bài 1: Cho một đường tròn, O là tâm đường tròn, một đường kính $AB$  với một dây cung $CD$ giao cắt với đường kính $AB$ tại điểm M ($CD$ nhận M làm trung điểm). Qua M lấy E đối xứng với A. Hỏi:

a, $ACED$ thuộc hình gì? Giải thích lý do?

b, Giả sử bán kính đường tròn có độ lớn bằng 6,5cm và độ dài đoạn thẳng $MA$ là 4cm, hãy tính độ dài đoạn thẳng $CD$?

Hướng dẫn giải bài tập:

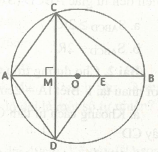
a, Vì $CD$ tạo với đường kính $AB$ một góc có độ lớn bằng $90^0$ và $CD$ nhận M làm trung điểm 

=> $MC=MD$

Qua điểm M, E đối xứng với A => $ME=MA$

Xét trong tứ giác $ACED$ có $AE$ và $CD$ là hai đường chéo, ta có:

+ $AE\perp CD$

+ $CM=MD$, $AM=ME$

=> Tứ giác $ACED$ là hình thoi (vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường chéo)

b, Vì điểm C thuộc đường tròn tâm O nên $\widehat{ACB} = 90^0$ (góc chắn nửa đường tròn)

Sử dụng hệ thức lượng trong tam giác vuông đối với $\Delta ACB$ ta có:

$MC^2=MA.MB$ = $MA.(AB-MA)$ => $MC^2=4.(2.6,6-4)=36$

=> $MC=\sqrt{36}=6(cm)$

Vì M là trung điểm của $CD$ => $CD$ = $2.MC$ = $2.6=12$ (cm)

Bài 2: Cho một đường tròn, O là tâm đường tròn với độ dài bánh kính là 25cm, một dây cung $AB$ có độ dài là 40cm. Trong phạm vi đường tròn, kẻ một dây cung $CD$ với điều kiện là $CD//AB$ và cách $AB$ một khoảng bằng 22cm. Hỏi dây CD có độ dài bằng bao nhiêu?

Hướng dẫn giải bài tập: 

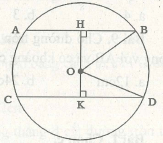
Ta có: Trong tam giác $OHB$ có $\widehat{H}=90^0$, sử dụng định lý Py-ta-go cho tam giác vuông:

$OH^2=OB^2-HB^2$ = $25^2-20^2=225$ => $OH=\sqrt{225}=15$ (cm)

Lại có: $OK=HK-OH$ => $OK=22-15=7(cm)$

Trong tam giác $OKD$ có $\widehat{K}=90^0$, sử dụng định lý Py-ta-go cho tam giác vuông:

$KD^2=OD^2-OK^2$ = $25^2-7^2=576$ => $KD=\sqrt{576}=24$ (cm)

Vì K là trung điểm của đoạn thẳng $CD$ nên $CD=2.KD$ => $CD=2.24=48(cm)$

Tham khảo thêm >>> Giải toán 9 Đường kính và dây của đường tròn (sách giáo khoa)

Cunghocvui đã gửi tới các bạn bài lý thuyết và dạng các bài tập về đường kính và dây của đường tròn thông qua bài viết đường kính và dây của đường tròn. Nếu có đóng góp hay thắc mắc gì về bài viết toán 9 đường kính và dây của đường tròn, các bạn hãy để lại comment dưới phần bình luận nhé!