Giải bài 67 trang 31 - Sách giáo khoa Toán 8 tập 1
Đề bài
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:
a) (x\(^3\) – 7x + 3 – x\(^2\)) : (x – 3) ; b) (2x\(^4\) – 3x\(^3\) – 3x\(^2\) – 2 + 6x) : (x\(^2\) – 2)
Hướng dẫn giải
a) (x\(^3\) – 7x + 3 – x\(^2\)) : (x – 3) = (x\(^3\) – x\(^2\) - 7x +3) : (x – 3)
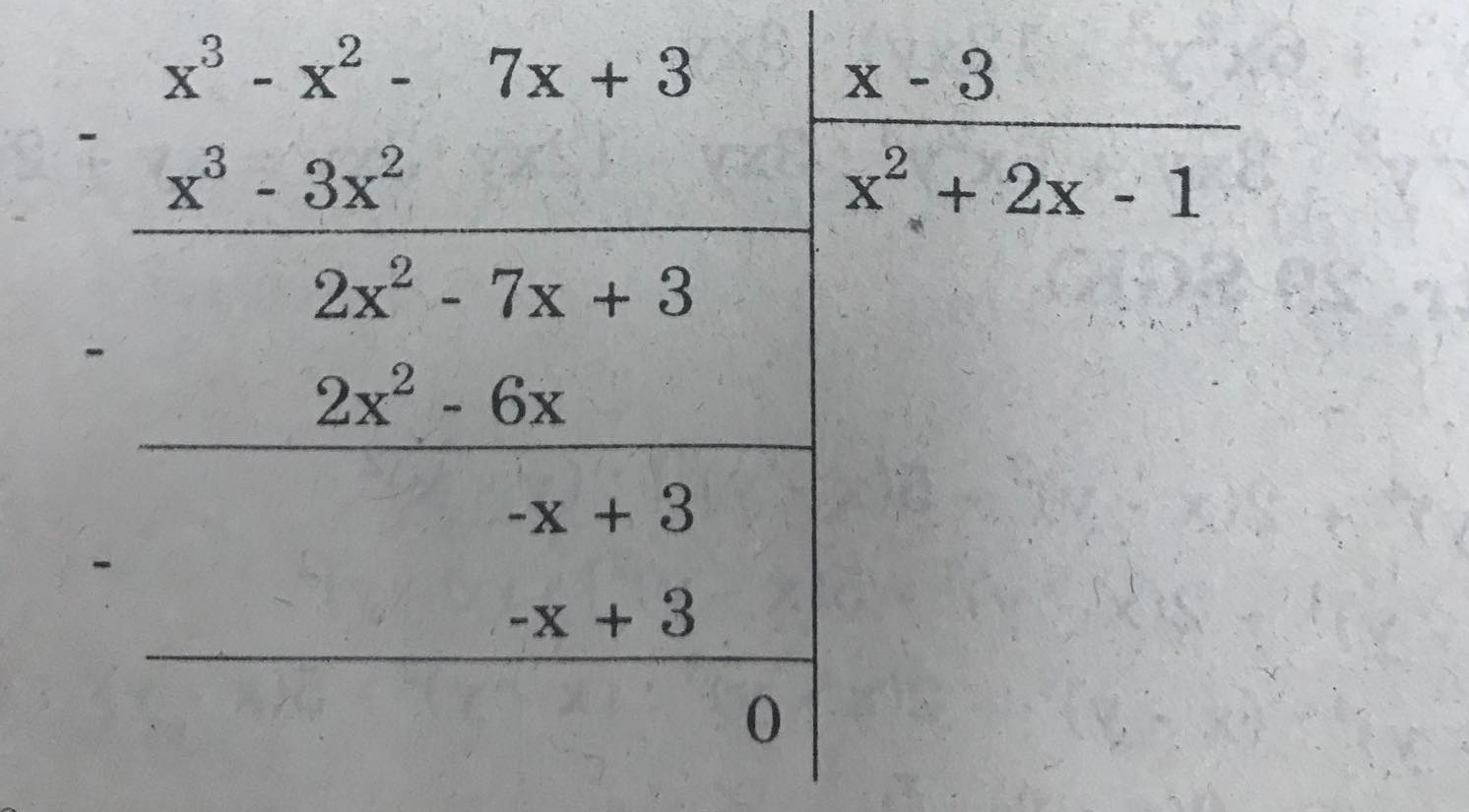
Vậy : (x\(^3\) – x\(^2\) - 7x +3) : (x – 3) = x\(^2\) + 2x - 1
b) (2x\(^4\) – 3x\(^3\) – 3x\(^2\) – 2 + 6x) : (x\(^2\) – 2)
= (2x\(^4\) – 3x\(^3\) – 3x\(^2\) + 6x - 2) : (x\(^2\) – 2)
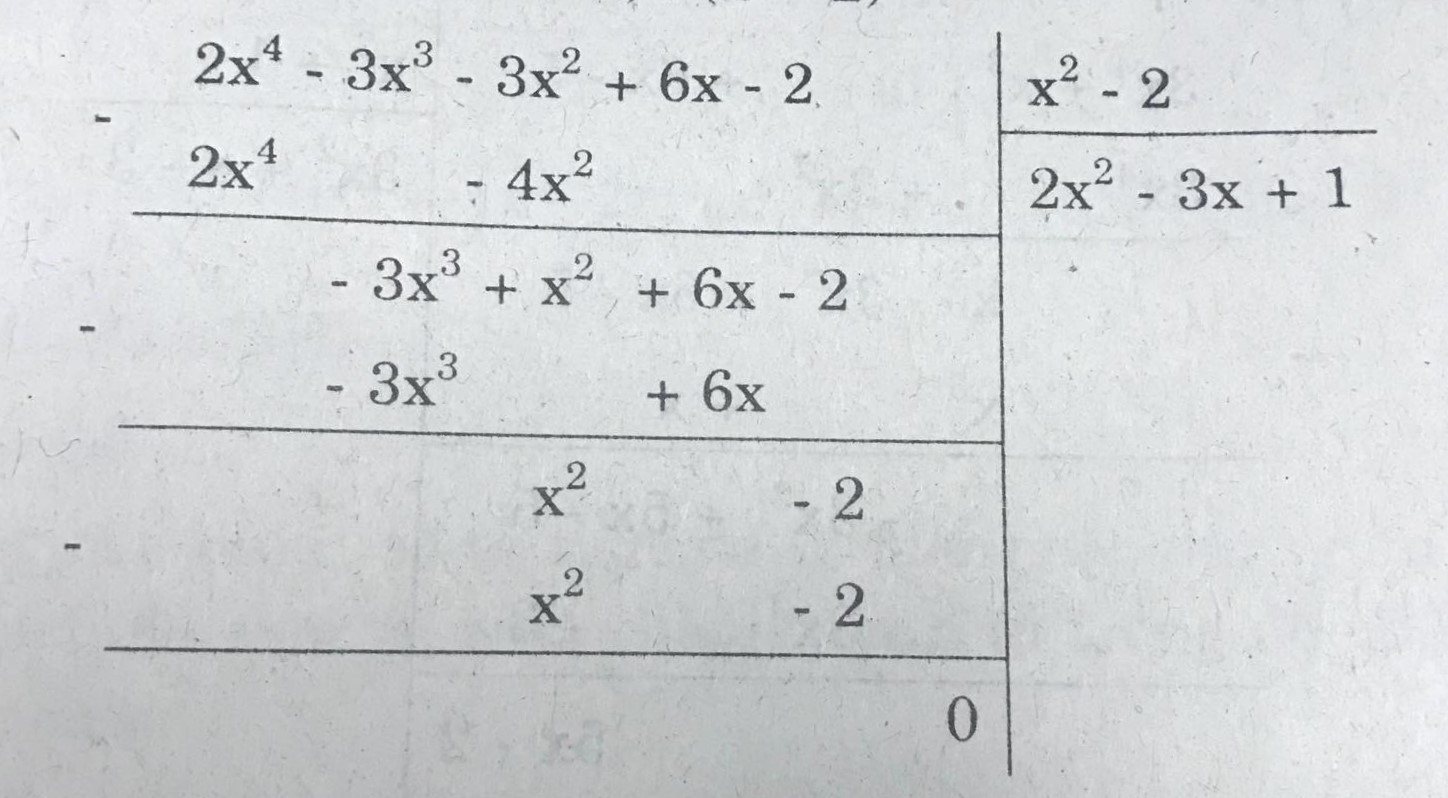
Vậy : (2x\(^4\) – 3x\(^3\) – 3x\(^2\) + 6x - 2) : (x\(^2\) – 2) = \(2x^2 - 3x +1\)

