Giải bài 34 trang 128 - Sách giáo khoa Toán 8 tập 1
Đề bài
Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.
Hướng dẫn giải
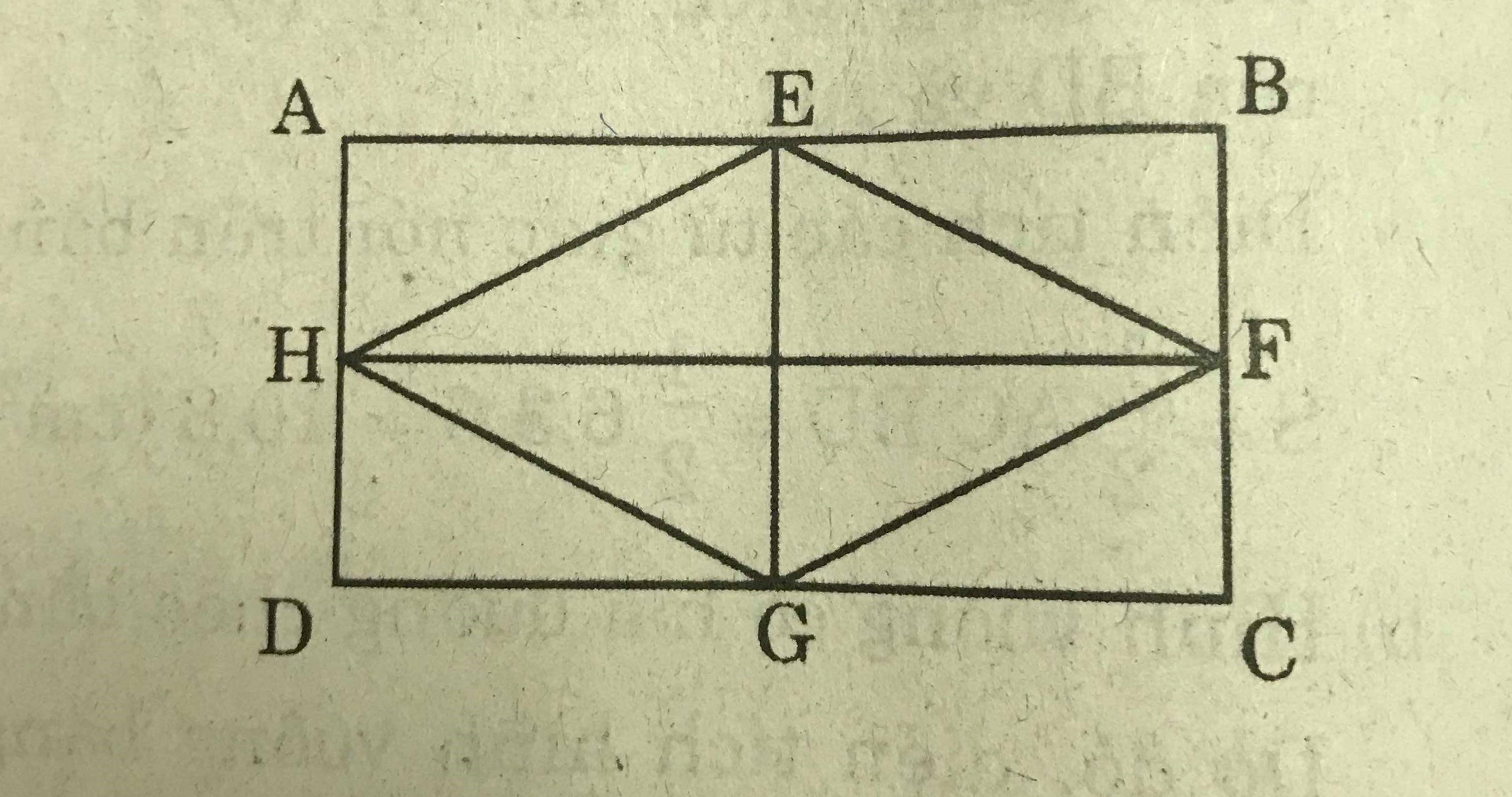
Gọi E, F, G, H là trùn điểm các cạnh AB, BC , CD , DA của hình chữ nhật ABCD.
Xét \(\triangle\)AEH và \(\triangle\)BEF có :
EA = EB (gt)
HA = BF (gt)
Nên \(\triangle\)AEH = \(\triangle\)BEF (c.g.c)
Chứng minh tương tự : \(\triangle\)DGH = \(\triangle\)CGF ; \(\triangle\)AEH = \(\triangle\)DGH
Do đó : \(\triangle\)AEH = \(\triangle\)BEF = \(\triangle\)CGF = \(\triangle\)DGH
Nên : EH = EF = FG = GH.
Suy ra : EFGH là hình thoi.
\(S_{EFGH}=S_{ABFH}\) ( cùng bằng \(2S_{EHF}\))
\(=\dfrac{1}{2}S_{ABCD}=\dfrac{1}{2}AD.DC=\dfrac{1}{2}EG.HF\)
Điều này chứng tỏ diện tích hình thoi bằng nửa diện tích hình chữ nhật

