Bài 74 trang 106 SGK Toán 8 tập 1
Đề bài
Hai đường chéo của một hình thoi bằng \(8cm\) và \(10cm\). Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) \(6cm\); (B) \(\sqrt {41} cm\)
(C) \(\sqrt {164} cm\) (D) \(9cm\) ?
Hướng dẫn giải
Áp dụng tính chất của hình thoi: Hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường
Lời giải chi tiết
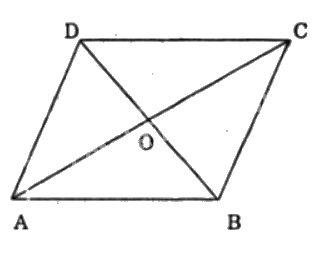
Xét bài toán tổng quát:
\(ABCD\) là hình thoi, \(O\) là giao điểm hai đường chéo.
Theo tính chất của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
\( \Rightarrow \left\{ \begin{array}{l}
OA = \frac{{AC}}{2}\\
OB = \frac{{B{\rm{D}}}}{2}
\end{array} \right.\)
Áp dụng định lí Pytago vào tam giác vuông \(ABO\) ta có:
\(\eqalign{
& A{B^2} = O{A^2} + O{B^2} \cr&\;\;\;\;\;\;\;\;= {\left( {{1 \over 2}AC} \right)^2} + {\left( {{1 \over 2}BD} \right)^2} \cr
& \Rightarrow AB = \sqrt {{{\left( {{1 \over 2}AC} \right)}^2} + {{\left( {{1 \over 2}BD} \right)}^2}}\cr&\;\;\;\;\;\;\;\;\;\;\; = \sqrt {{4^2} + {5^2}} = \sqrt {41} cm \cr} \)
Vậy (B) đúng.

