Bài 55 trang 25 SGK Toán 8 tập 1

Đề bài

Tìm \(x\), biết:

a)  \({x^3} - {1 \over 4}x = 0\);                     

b) \({(2x - 1)^2} - {(x + 3)^2} = 0\);

c) \({x^2}(x - 3) + 12 - 4x = 0\).

Hướng dẫn giải

- Phân tích vế trái thành nhân tử rồi áp dụng tính chất: 

\(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}
A = 0\\
B = 0
\end{array} \right.\)

Lời giải chi tiết

a) Ta có:

\(\eqalign{
& {x^3} - {1 \over 4}x = 0 \Rightarrow x\left( {{x^2} - {1 \over 4}} \right) = 0 \cr
& \Rightarrow x\left( {{x^2} - {{\left( {{1 \over 2}} \right)}^2}} \right) = 0 \cr
& \Rightarrow x\left( {x - {1 \over 2}} \right)\left( {x + {1 \over 2}} \right) = 0 \cr
& \Rightarrow \left[ \matrix{
x = 0 \hfill \cr
\left( {x - {1 \over 2}} \right) = 0 \Rightarrow x = {1 \over 2} \hfill \cr
\left( {x + {1 \over 2}} \right) = 0 \Rightarrow x = - {1 \over 2} \hfill \cr} \right. \cr} \)

Vậy \(x=0,x={1\over 2},x=-{1\over2}\)

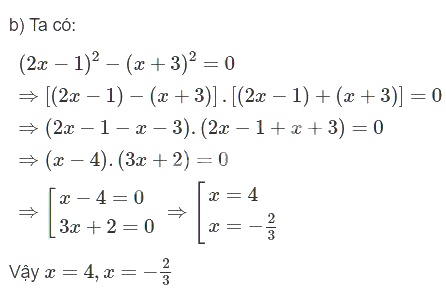
c) Ta có:

\(\eqalign{
& {x^2}(x - 3) + 12 - 4x = 0 \cr
& \Rightarrow {x^2}(x - 3) - 4(x - 3) = 0 \cr
& \Rightarrow (x - 3)({x^2} - 4) = 0 \cr
& \Rightarrow (x - 3)(x - 2)(x + 2) = 0 \cr
& \Rightarrow \left[ \matrix{
x = 3 \hfill \cr
x = 2 \hfill \cr
x = - 2 \hfill \cr} \right. \cr} \)

Vậy \( x=3,x=2,x=-2\)