Bài 4 trang 12 SGK Hình học 10
Đề bài
Cho tam giác \(ABC\). Bên ngoài tam giác vẽ các hình bình hành \(ABIJ, BCPQ, CARS\). Chứng minh rằng \(\overrightarrow{RJ} + \overrightarrow{IQ} + \overrightarrow{PS}= \overrightarrow{0}.\)
Hướng dẫn giải
Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:
\(+ )\;\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\( + )\;\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết
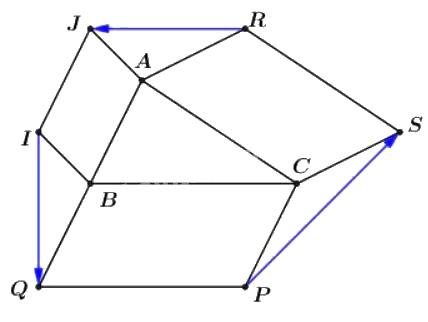
Ta xét tổng:
\(\overrightarrow{RJ} + \overrightarrow{JI} +\overrightarrow{IQ} + \overrightarrow{QP}+\overrightarrow{PS}+ \overrightarrow{SR} \)\(= \overrightarrow{RR}= \overrightarrow{0}\)(1)
Mặt khác, ta có \(ABIJ, BCPQ\) và \(CARS\) là các hình bình hành nên:
\(\overrightarrow{JI} = \overrightarrow{AB}\)
\(\overrightarrow{QP} = \overrightarrow{BC}\)
\(\overrightarrow{SR}= \overrightarrow{CA}\)
\(\Rightarrow \overrightarrow{JI}+\overrightarrow{QP}+\overrightarrow{SR}\)\(= \overrightarrow{AB}+ \overrightarrow{BC}+\overrightarrow{CA}= \overrightarrow{AA}= \overrightarrow{0}\) (2)
Từ (1) và (2) suy ra : \(\overrightarrow{RJ} + \overrightarrow{IQ} + \overrightarrow{PS}\)\(= \overrightarrow{0}.\) (đpcm)

