Lý thuyết Dấu của nhị thức bậc nhất đầy đủ nhất

Dấu của nhị thức bậc nhất là một kiến thức trọng tâm của chương trình Toán học 10. Cunghocvui gửi tới các bạn bài viết lý thuyết và các dạng bài tập toán 10 dấu của nhị thức bậc nhất đầy đủ và chi tiết. Mời các bạn tham khảo!

A. Tóm tắt lý thuyết bài giảng dấu của nhị thức bậc nhất

1. Định lý về dấu của nhị thức bậc nhất

- Nhị thức bậc nhất được cho dưới dạng công thức \(f(x) = ax + b\) trong đó a được gọi là hệ số góc, b được gọi là hệ số tự do và có điều kiện \(a\neq 0\)

a, Dấu của nhị thức bậc nhất:

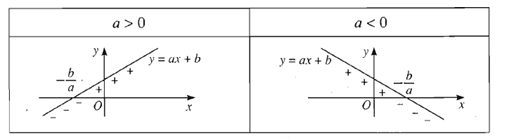
+ Dấu của nhị thức bậc nhất \(f(x) = ax + b\) với điều kiện \(a\neq 0\) sẽ có dấu cùng dấu với hệ số a khi và chỉ khi khoảng giá trị \((\dfrac{-b}{a};+\infty )\) chứa x

+ Dấu của nhị thức bậc nhất \(f(x) = ax + b\) với điều kiện \(a\neq 0\) sẽ có dấu ngược dấu với hệ số a khi và chỉ khi khoảng giá trị \((-\infty;\dfrac{-b}{a} )\) chứa x

Từ định lý về dấu của nhị thức bậc nhất, ta rút ra được bảng xét dấu của nhị thức bậc nhất như sau:

b, Nhận xét dấu của các tích, thương của các nhị thức bậc nhất

Nếu f(x) là tích hoặc thương của một hay nhiều những nhị thức bậc nhất. Muốn xét dấu của nhị thức bật nhất f(x), ta có thể xét dấu của từng nhân tử trong f(x) rồi sẽ xét dấu chung cho toàn f(x) như thông thường

2. Từ định lý về Toán 10 dấu nhị thức bậc nhất, áp dụng vào các bài tập giải bất phương trình

Bài tập về giải bất phương trình hay có thể nói cách khác là xét xem khi x nhận những giá trị nào thì biểu thức \(f(x) = ax + b\) sẽ lớn hơn 0 (nhận giá trị dương) hoặc ngược lại, khi x nhận những giá trị nào thì biểu thức \(f(x) = ax + b\) sẽ nhỏ hơn 0 (nhận những giá trị âm).

a, Bài tập giải bất phương trình tích, bất phương trình mà mẫu chứa ẩn

- Cách làm chung: 

+ Tìm điều kiện để mẫu thức khác 0 (phân thức được xác định) và tiến hành quy đồng mẫu thức các phân thức

+ Lập bảng xét dấu các nhị thức bậc nhất và rút ra kết luận nghiệm

b, Bài tập giải bất phương trình có dấu giá trị tuyệt đối chứa ẩn

- Cách làm chung

+ Dựa vào tính chất và định lý về giá trị tuyệt đối để giải bài tập bất phương trình có dạng cho bởi \(\left | f(x) \right |\leq a\) và \(\left | f(x) \right |\geq a\) với điều kiện của hệ số \(a>0\)

- Với hệ số a > 0 ta có một số nhận xét sau:

+ \(\left | f(x) \right |\leq a\) <=> \(-a\leq f(x)\leq a\)

+ \(\left | f(x) \right |\geq a\) <=> \(f(x)\leq -a\) hoặc \(f(x)\geq a\)

B. Các bài tập dấu của nhị thức bậc nhất

1. Dạng 1: Bài tập giải bất phương trình và biện luận dấu bất phương trình bậc nhất

a, Phương pháp giải dấu của nhị thức bậc nhất

- Cho một nhị thức bậc nhất \(ax+b <0\). Từ đó rút ra \(ax <-b\). Nhận xét các trường hợp sau:

+ Với a mang giá trị lớn hơn 0 (a > 0): S = \((-\infty;\dfrac{-b}{a} )\)

+ Với a mang giá trị nhỏ hơn 0 (a < 0): S = \((\dfrac{-b}{a};+\infty )\)

+ Với a mang giá trị bằng 0 (a = 0): \(0x <-b\)

Với b mang giá trị dương \((b\geq 0)\) tập giá trị x sẽ không có phần tử 

Với b mang giá trị âm hoặc bằng 0 \((b\leq 0)\) thì tập giá trị x sẽ có vô số phần tử (S = R)

b, Các bài tập dấu của nhị thức bậc nhất

Bài 1: Biện luận nghiệm và giải một số bất phương trình bậc nhất sau:

a, \(m^2(x-2)> x-2m\)

b, \(\dfrac{x-m}{2m}+\dfrac{x-1}{m}\leq \dfrac{x+1}{2}\)

c, \((x+m)(x-m+2)\geq 0\)

d, \(\dfrac{(m-2)x-m+2}{x-m}\leq 0\)

Bài 2: Giải và biện luận nghiệm các bất phương trình sau:

a, \(\sqrt{x-m}(2x-m+2)\leq 0\)

b, \(\sqrt{x-1}(x-2m)-\dfrac{x^2-mx+m^2-3}{\sqrt{x-1}}> 0\)

2. Dạng 2: Biện luận nghiệm và giải bất phương trình mang dấu giá trị tuyệt đối

a, Cách giải dấu của nhị thức bậc nhất

- Vận dụng tính chất và định lý về dấu giá trị tuyệt đối:

+ \(\left | f(x) \right |\leq a\) <=> \(-a\leq f(x)\leq a\)

+ \(\left | f(x) \right |\geq a\) <=> \(f(x)\leq -a\) hoặc \(f(x)\geq a\)

b, Các bài tập dấu của nhị thức bậc nhất

Bài 1: Giải và biện luận nghiệm của một số bất phương trình sau:

a, \(\left | 1-x \right |+\left | x-2 \right |> \left | x-4 \right |\)

b, \(\left | mx-1 \right |< 2m-2\)

c, \(\left | x \right |-\left | x-2 \right |< 2\left | x-4 \right |\)

Tham khảo thêm >>> Giải bài tập sách giáo khoa Toán 10 Dấu của nhị thức bậc nhất

Với bài giảng dấu của nhị thức bậc nhất, Cunghocvui đã mang đến cho các bạn lý thuyết và các dạng bài tập đầy đủ và chi tiết. Nếu có đóng góp gì cho bài giảng dấu của nhị thức bậc nhất hãy để lại comment dưới phần bình luận nhé!