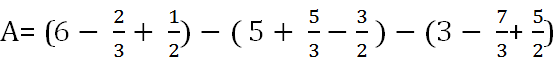Giải bài 10 trang 10 - Sách giáo khoa Toán 7 tập 1
Đề bài
Hãy tính giá trị A theo hai cách
Cách 1: Trước hết tính giá trị từng biểu thức trong ngoặc
Cách 2: Bỏ dấu ngoặc rồi nhóm các số thích hợp
Hướng dẫn giải
Hướng dẫn:
Cách 1 : Trước hết, tính giá trị của từng biểu thức trong ngoặc.
Cách 2: Bỏ ngoặc rồi nhóm các số hạng thích hợp.
Với mọi x, y \(\in\) Q thì -(x + y - z) = - x - y + z.
Nhóm các số hạng có cùng mẫu số với nhau.
Giải:
Cách 1 :
\(A = (6-\dfrac{2}{3} + \dfrac{1}{2})-(5+\dfrac{5}{3}-\dfrac{3}{2})-(3-\dfrac{7}{3}+\dfrac{5}{2})\)
\(=(\dfrac{36}{6}-\dfrac{4}{6} + \dfrac{3}{6})-(\dfrac{30}{6}+\dfrac{10}{6}-\dfrac{9}{6})-(\dfrac{18}{6}-\dfrac{14}{6}+\dfrac{15}{6})\)
\(= (\dfrac{36-4+3}{6})-(\dfrac{30+10-9}{6}) - (\dfrac{18-14+15}{6})\)
\(= \dfrac{35}{6}-\dfrac{31}{6}-\dfrac{19}{6}= \dfrac{-15}{6}=\dfrac{-5}{2}=-2\dfrac{1}{2}.\)
Cách 2 :
\(A = (6-\dfrac{2}{3} + \dfrac{1}{2})-(5+\dfrac{5}{3}-\dfrac{3}{2})-(3-\dfrac{7}{3}+\dfrac{5}{2})\)
\(= 6- \dfrac{2}{3} + \dfrac{1}{2} -5 -\dfrac{5}{3} + \dfrac{3}{2}-3 + \dfrac{7}{3}-\dfrac{5}{2}.\)
\(= (6-5-3) -(\dfrac{2}{3} +\dfrac{5}{3} - \dfrac{7}{3}) + ( \dfrac{1}{2}+ \dfrac{3}{2} - \dfrac{5}{2})\)
\(= -2-0-\dfrac{1}{2} = -2\dfrac{1}{2}.\)