Bài 4 trang 121 SGK Hình học 11

Đề bài

Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và có góc \(\widehat{ BAD} = 60^0\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Đường thẳng SO vuông góc với mặt phẳng (ABCD) và \(SO = {{3a} \over 4}\) . Gọi \(E\) là trung điểm của đoạn \(BC\) và \(F\) là trung điểm của đoạn \(BE\).

a) Chứng minh mặt phẳng \( (SOF)\) vuông góc với mặt phẳng \((SBC)\)

b) Tính các khoảng cách từ \(O\) và \(A\) đến mặt phẳng \((SBC)\)

Hướng dẫn giải

a) Chứng minh \(BC \bot \left( {SOF} \right)\).

b) Dựng và tính khoảng cách từ O đến mặt phẳng \((SBC)\). Chứng minh \(d\left( {A;\left( {SBC} \right)} \right) = 2d\left( {O;\left( {SBC} \right)} \right)\).

Lời giải chi tiết

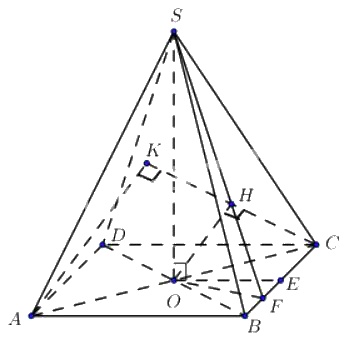
a) Theo giả thiết \(\widehat{ BAD} = 60^0\) nên theo tính chất của hình thoi \(\widehat{ BCD} = 60^0\) hay tam giác \(BDC\) đều.

Xét tam giác \(BOE\) có \(BO=BE=\dfrac{{a}}{2}\) và \(\widehat{ OBE} = 60^0\) nên tam giác \(BOE\) đều

Do đó \(OF\) là đường cao và ta được \(OF ⊥BC\). 

\(\left\{ \begin{array}{l}
SO \bot \left( {ABCD} \right) \Rightarrow BC \bot SO\\
BC \bot OF
\end{array} \right. \Rightarrow BC \bot \left( {SOF} \right)\\ \Rightarrow BC \bot SF\)

Mà \(BC ⊂ (SBC)\Rightarrow (SOF) ⊥ (SBC)\)

b) Vì \((SOF) ⊥ (SBC)\) và hai mặt phẳng này giao nhau theo giao tuyến \(SF\) nên nếu từ điểm \(O\) ta kẻ \(OH⊥SF\) thì \(OH⊥(SBC)\) và \(OH\) chính là khoảng cách từ \(O\) đến \((SBC)\)

Ta có:

\(\begin{array}{l}SO = \frac{{3a}}{4};\,\,OF = \dfrac{{a\sqrt 3 }}{4}\\ \Rightarrow SF = \sqrt {S{O^2} + O{F^2}} = \dfrac{{a\sqrt 3 }}{2}\\OH.SF = SO.OF \Rightarrow OH = \dfrac{{SO.OF}}{{SF}} = \dfrac{{3a}}{8}\end{array}\)

Gọi \(K\) là hình chiếu của \(A\) trên \((SBC)\), ta có \(AK//OH\)

Trong \(ΔAKC\) thì \(OH\) là đường trung bình, do đó: \(AK = 2OH \Rightarrow AK =\dfrac{{3a}}{4}\).

Vậy \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{3a}}{4}\)