Bài 3 trang 60 SGK Hình học 11

Đề bài

Cho tứ diện \(ABCD\). Gọi \(M, N\) lần lượt là trung đểm của các cạnh \(AB, CD\) và \(G\) là trung điểm của đoạn \(MN\)

a) Tìm giao điểm \(A'\) của đường thẳng \(AG\) và mặt phẳng \((BCD)\)

b) Qua \(M\) kẻ đường thẳng \(Mx\) song song với \(AA'\) và \(Mx\) cắt \((BCD)\) tại \(M'\). Chứng minh \(B, M', A'\) thẳng hàng và \(BM' = M'A' = A'N\).

c) Chứng minh \(GA = 3 GA'\).

Hướng dẫn giải

a) Trong \((ABN)\): Gọi \(A'=AG  \cap BN\).

b) Sử dụng định lí đường trung bình của tam giác.

c) Sử dụng tính chất đường trung bình của tam giác.

Lời giải chi tiết

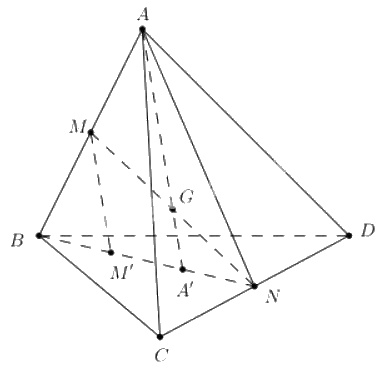
a) Trong \((ABN)\): Gọi \(A'=AG  \cap BN\)

\( \Rightarrow A' \in BN\), \(BN \subset (BCD)\).

\( \Rightarrow A' \in (BCD) \Rightarrow  A' = AG \cap (BCD)\).

b) \(MM'//AA'\) mà \(AA'\subset (ABA')\) do đó: \(MM'\subset (ABA')\)

Mặt khác \(M'\in (BCD)\) nên \(M'\) thuộc giao tuyến \(A'B\) của \((ABA')\) và \((DBC)\) \(\Rightarrow\) B, M', A' thẳng hàng.

*) Xét tam giác \(NMM'\) có:

+) \(G\) là trung điểm của \(NM\).

+) \(GA'//MM'\)

\(\Rightarrow A'\) là trung điểm của \(NM'\)

Xét tam giác \(BAA'\) có:

+) \(M \) là trung điểm của \(AB\) 

+) \(MM'//AA'\)

\(\Rightarrow M'\) là trung điểm của \(BA'\)

Do đó: \(BM'=M'A'=A'N\).

c) Ta có \(GA'={1\over 2} MM'\)

             \(MM'={1\over 2} AA'\)

\(\Rightarrow GA'={1\over 4} AA'\Rightarrow GA=3 GA'\).