Bài 2 trang 24 SGK Hình học 11
Đề bài
Cho hình chữ nhật \(ABCD\). Gọi \(E, F, H, K, O, I, J\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DA, KF, HC, KO\). Chứng minh hai hình thang\(AEJK\) và \(FOIC\) bằng nhau.
Hướng dẫn giải
Gọi L là trung điểm của OF, thực hiện liên tiếp hai phép biến hình sau:
- Phép đối xứng trục E.
- Phép tịnh tiến theo vector BF.
Các phép tịnh tiến và phép đối xứng trục hình không làm thay đổi khoảng cách giữa hai điểm bất kì.
Lời giải chi tiết
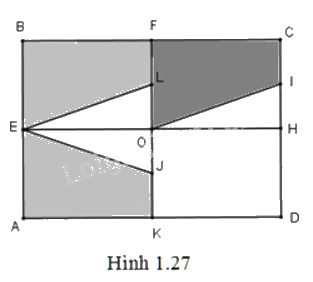
Gọi \(L\) là trung điểm của đoạn thẳng \(OF\). Ta thấy phép đối xứng qua đường thẳng \(EH\) biến hình thang \(AEJK\) thành hình thang \(BELF\).
Phép tịnh tiến theo vectơ \(BF\) biến hình thang \(BELF\) thành hình thang \(FOIC\).
Như vậy phép dời hình có được bằng cách thực hiện liên tiếp phép biến hình trên, sẽ biến hình thang \(AEJK\) thành hình thang \(FOIC\). Do đó hai hình thang \(AEJK\) và \(FOIC\) bằng nhau.

