Lý thuyết chung về lũy thừa và một số bài tập tham khảo trong toán học

Lũy thừa là gì? Khái niệm lũy thừa cúng như các dạng bài toán liên quan là một trong những chủ đề quan trọng trong chương trình Đại số của các em học sinh trung học phổ thông. Cùng chúng tôi tìm hiểu cụ thể về lũy thừa qua bài viết dưới đây nhé!

I. Lũy thừa là gì?

Lũy thừa là một phép toán thực hiện trên hai số a, b, ký hiệu là \(a^b\), đọc là lũy thừa bậc b của a, khi đó ta gọi a là cơ số còn b được gọi là số mũ.

Hàm số lũy thừa là các hàm số dạng \(y=x_α(α∈R)\). Các hàm số lũy thừa có tập xác định khác nhau, tùy theo α: 

• Nếu α nguyên dương thì tập các định là R.
• Nếu α nguyên âm hoặc α=0 thì tập các định là R\{0}.
• Nếu α không nguyên thì tập các định là \((0;+∞)(0;+∞)\).

Tập xác định của hàm số lũy thừa: Hàm số \(y=\sqrt x\) có tập xác định là \([0;+∞)[0;+∞)\), hàm số \(y=\sqrt[3]{x}\) có tập xác định R, trong khi đó các hàm \(y=x^{\dfrac{1}{2}},y=x^{\dfrac{1}{3}}\) đều có tập xác định \((0;+∞)(0;+∞)\).. Vì vậy \(y=\sqrt x, y=x^{\dfrac{1}{2}}\) hay \(y=\sqrt[3]x , y=x^{\dfrac{1}{3}}\) là những hàm lũy thừa khác nhau.

II. Tính chất của lũy thừa

Tính chất cơ bản:

• \(a^n = a {\displaystyle \times } a {\displaystyle \times } a {\displaystyle \times }... {\displaystyle \times } a\) với n chữ số a
• \({\displaystyle a^{-n}={\frac {1}{a^{n}}}={\dfrac {1}{a\times a\times a\times ...a}}}\)
• \(0^n = 0 (n > 0)\)
• \(1^n = 1\)
• \(a^0 = 1\)
• \(a^1 = a\)
• \({\displaystyle a^{-1}={\dfrac {1}{a}}}\)

Tính chất thường gặp:

• \( a^{m + n} = a^m {\displaystyle \times } a^n\)
• \({\displaystyle a^{m-n}={\dfrac {a^{m}}{a^{n}}}}\) với mọi a ≠ 0
• \({\displaystyle a^{m.n}=(a^{m})^{n}}\)
• \({\displaystyle a^{m^{n}}=a^{(m^{n})}}\)
• \({\displaystyle (a\times b)^{n}=a^{n}\times b^{n}}\)
• \({\displaystyle ({\dfrac {a}{b}})^{n}={\dfrac {a^{n}}{b^{n}}}}\)
• \({\displaystyle a^{\dfrac{m}{n}}=\left(a^{m}\right)^{\dfrac{1}{n}}={\sqrt[{n}]{a^{m}}}}\)
• \({\displaystyle a^{x}=e^{x. \ln a}\,}\)
• \({\displaystyle e^{ix}=\cos x+i. \sin x}\)

III. Công thức lũy thừa

Chuyên đề về lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của a là gì? Cho n là một số nguyên dương, với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a: \(a^{n}=\overset{\underbrace{a\times a…\times a}}{n}\) .
• Với a # 1. Lũy thừa của số a # 0 với số mũ -1 là số nghịch đảo của nó:  \(a^{-1}=\dfrac{1}{a}\)
• Lũy thừa của a với số mũ nguyên âm m= -n là: \(a^{m}=a^{-n}=\dfrac{1}{a^{n}}\)
• Lũy thừa với số mũ 0 của số a: \(1=\dfrac{a^{n}}{a^{n}}=a^{n-n}=a^{0}\)
• Lũy thừa của 0 và 1: \(0^m=0, 1^m=1\)

Chuyên đề lũy thừa với số mũ thực:

• Vì mỗi số thực có thể được tiệm cận bởi các số hữu tỉ. Do đó, lũy thừa với mũ số thực x có thể được xác định qua công thức sau: \(b^{x}=\lim_{r\to x}b^{r}\) ( trong đó r tiến tới x chỉ trong các giá trị hữu tỷ của r )
• Lũy thừa với số mũ thực cũng thường được địng nghĩa bằng sử dụng Logarit thay cho giới hạn của các số hữu tỷ:  \(a^{x}=e^{x.lna}\), với mọi số thực dương a
• Lũy thừa mũ số phức e: \(e^{ix}=cosx+i.sinx\). Sau đó với số phức \(z=x+y.i\) ta có: \(e^{z}=e^{x+yi}=e^{x}+e^{yi}=e^{x}(cosy+i.siny)\)

Lũy thừa của một số hữu tỉ:

Cho số thực dương và số hữu tỷ \(\dfrac{m}{n}\), ta có lũy thừa với số mũ hữu tỷ được xác định như sau:

\(a^{\dfrac{m}{n}}=(a^{m})^{\dfrac{1}{n}}=\sqrt[n]{a^{m}}\)

Định nghĩa này có thể mở rộng cho các số thực âm mỗi khi căn thức có nghĩa.

IV. Một số dạng bài tập tham khảo:

Bài 1:Vẽ đồ thị của hàm lũy thừa \(y=\sqrt3^x\). Dựa vào đồ thị, hãy giải thích các bất phương trình sau:

a) \( (\sqrt3)^x \le 1\)                   b) \( (\sqrt3)^x \ge 3\)

Lời giải

TXĐ: D=RD=R

Hàm số đồng biến trên R.

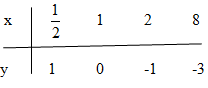
a) \((\sqrt3)^x≤1⇔x≤0\) (ứng với những điểm trên đồ thị có tung độ lớn hơn 1)
b) \((\sqrt3)^x \ge 3⇔x\ge2\) (ứng với những điểm trên đồ thị có tung độ lớn hơn 3).

Bài 2: Từ tính chất của lũy thừa với số mũ nguyên dương, chứng minh:

\(\sqrt[n]{ab}=\sqrt[n]{a}.\sqrt[n]{b}\) ( \(a≥0,b≥0a,\) n nguyên dương)

Lời giải: 

Cách 1:

Theo tính chất của lũy thừa với số mũ nguyên dương, ta có:

\((\sqrt[n]{a}.\sqrt[n]b)^n=(\sqrt[n]a)^n.(\sqrt[n]b)^n=ab\)

Do đó theo định nghĩa căn bậc n của một số, ta có \(\sqrt[n]{ab}=\sqrt[n]{a}.\sqrt[n]{b}\).

Cách 2:

Đặt \(\left\{\begin{array}{cc}\sqrt[n]a=x\\\sqrt[n]b=y\end{array}\right.\) thì \(\left\{\begin{array}{cc}x\ge 0\\y\ge 0\end{array}\right.\)

Ta có: \(\left\{\begin{array}{cc}a=x^n\\b=y^n\end{array}\right. \leftrightarrow ab=x^n.y^n\)

Áp dụng tính chất của lũy thừa với số mũ nguyên dương, ta có: \(ab=(xy)^n\)

\(\rightarrow xy=\sqrt[n]{ab}\rightarrow \sqrt[n]{ab}=\sqrt[n]a.\sqrt[n]b\)

V. Phương pháp làm các bài liên quan đến lũy thừa

Để làm tốt các bài tập liên quan các bạn có thể tham khảo một số phương pháp hữu hiệu sau đây:

Luyện tập các dạng bài thường xuyên. Cách tốt nhất là làm các bài tập trong sách giáo khoa liên quan đến phần lượng giác, từ đó sẽ tích lũy được kinh nghiệm làm bài cũng như nhớ được công thức và rút ngắn được thời gian làm bài. Muốn học tốt nó thì trước tiên bạn phải nắm bắt được những kiến thức nền tảng, tham khảo thêm tại lũy thừa. Đáp án chi tiết các bài tập lũy thừa lớp 12 giác tại đây:

Bài 1. Lũy thừa với số mũ hữu tỉ

Bài 2: Lũy thừa với mũ số thực

Bài 6. Hàm số lũy thừa

Và một số bài tập về lũy thừa lớp 6 Bài 7. Lũy thừa với số mũ tự nhiên. Nhân hai lũy thừa cùng cơ số. để ghi nhớ kiến thức công thức lũy thừa lớp 6, phần cơ bản.

Ngoài ra, để nâng cao khả năng giải các bài tập lượng giác ở các cấp cao hơn nhằm đạt được điển số tuyệt đối thì các em nên tham khảo các bài tập dạng nâng cao để hình thành nên tư duy sắc bén không chỉ trong các bài tập lượng giác mà còn các bài tập dạng liên quan khác. Việc làm quen với một dạng bài tập mới không phải chuyện một hai ngày có thể thành thạo mà nó là cả một quá trình luyện tập và trau dồi bản thân. 

Một phương pháp hữu hiệu khác là học theo nhóm hoặc tham khảo ý kiến thầy cô để nắm chắc trong tay cách tính lũy thừa và không bị bỡ ngỡ trước những dạng bài tập mới.

Trên đây là toàn bộ những công thức lũy thừa cần thiết để giúp bạn hoàn thành tốt những phần bài tập liên quan. Đây là một phần kiến thức nền tảng và gây không ít khó khăn cho các bạn học sinh, chính vì vậy chúng tôi hy vọng bài viết sẽ giúp ích các bạn trong suốt quá trình học tập của mình. Chúc các bạn đạt được điểm số cao!