Giải bài 59 trang 83 - Sách giáo khoa Toán 7 tập 2

Đề bài

Cho hình 57.

a) Chứng minh NS ⊥ LM

b) Khi góc LNP = $50^0$, hãy tính góc MSP và góc PSQ.

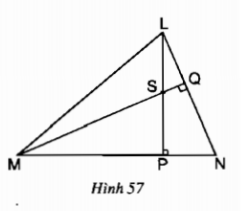
Hướng dẫn giải

a) LP ⊥ MN 

suy ra  LP là đường cao của ΔLMN 

MQ ⊥ NL

suy ra  MQ là đường cao của ΔLMN 

ΔLMN có hai đường cao LP, MQ cắt nhau tại S nên S là trực tâm của tam giác.

Do đó NS là đường cao của ΔLMN suy ra NS ⊥ LM.

b) ΔMQN vuông tại Q . Suy ra $\widehat{QNM} + \widehat{NMQ} = 90^o$

Suy ra $\widehat{NMQ} = 90^o - \widehat{QNM} = 90^o - 50^o =40^o.$

 ΔMSP vuông tại P . Suy ra  $\widehat{MSP} + \widehat{PMS} = 90^o$.

Suy ra $\widehat{MSP} = 90^o- \widehat{PMS} = 90^o - 40^o =50^o.$

Do đó  $\widehat{PMS} = 180^o - \widehat{MSP} = 180^o - 50^o = 130^o.$