Giải bài 44 trang 133 - Sách giáo khoa Toán 8 tập 1
Đề bài
Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.
Hướng dẫn giải
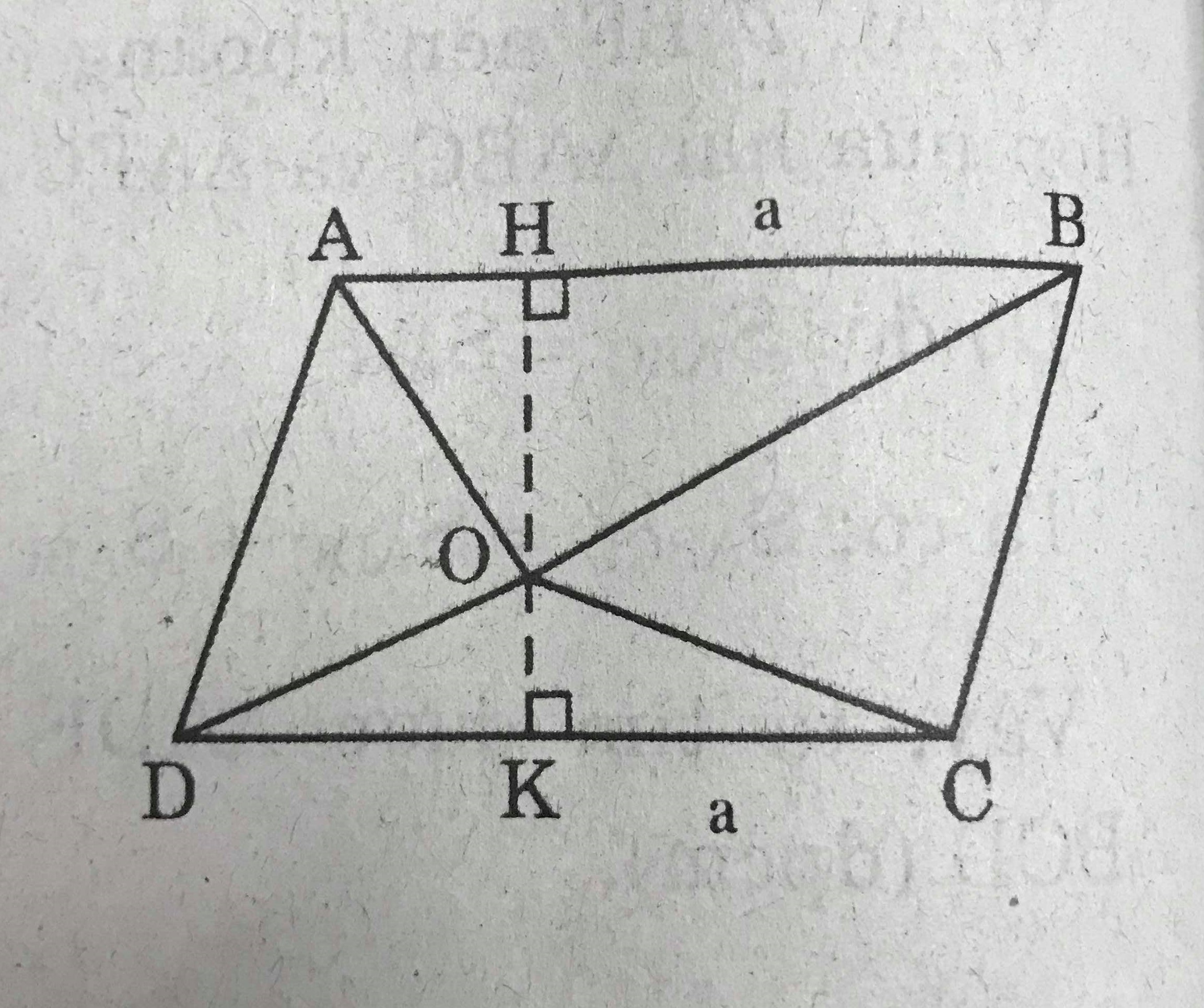
Đặt AB = CD = a
Kẻ OH \(\perp\) AB , OK \(\perp\) CD
Ta có : OH + OK = HK
\(S_{ABO}+S_{CDO}=\dfrac{1}{2}AB.OH+\dfrac{1}{2}CD.OK\)
\(=\dfrac{1}{2}a(OH+OK)=\dfrac{1}{2}a.HK=\dfrac{1}{2}S_{ABCD}\)
Vậy : \(S_{ABO}+S_{CDO}=S_{BCO}+S_{DAO}\)

