Công thức lượng giác lớp 10 chuẩn nhất

Ở bài viết này Cunghocvui sẽ gửi đến bạn học các công thức lượng giác lớp 10 cần nhớ, cùng với những cách học thuộc công thức lượng giác lớp 10 nhanh nhất. Hãy cùng đón đọc ở phần dưới nhé!

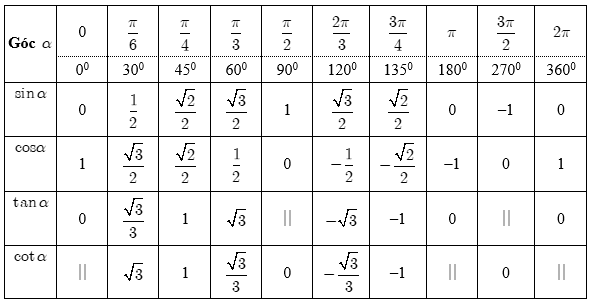
(Bảng giá trị góc lượng giác đặc biệt)

A. CÁC CÔNG THỨC LƯỢNG GIÁC LỚP 10 CẦN NHỚ

I. Các cung liên quan đặc biệt

1) Hai cung đối nhau (\(\alpha\) và  \(-\alpha\))

• \(cos(-\alpha)=cos\alpha\)
• \(sin(-\alpha)=-sin\alpha\)
• \(tan(-\alpha)=-tan\alpha\)
• \(cot(-\alpha)=-cot\alpha\)

2) Hai cung bù nhau (\(\alpha\) và \(​​\pi-\alpha\))

• \(sin(\pi-\alpha)=sin\alpha\)
• \(cos(\pi-\alpha)=-cos\alpha\)
• \(tan(\pi-\alpha)=-tan\alpha\)
• \(cot(\pi-\alpha)=-cot\alpha\)

3) Hai cung phụ nhau (\(\alpha\) và \(\dfrac {\pi}{2}-\alpha\))

• \(sin(\dfrac {\pi}{2}-\alpha)=cos\alpha\)
• \(cos(\dfrac {\pi}{2}-\alpha)=sin\alpha\)
• \(tan(\dfrac {\pi}{2}-\alpha)=cot\alpha\)
• \(cot(\dfrac {\pi}{2}-\alpha)=tan\alpha\)

4) Hai cung hơn, kém \(\pi\) (\(\alpha\) và \(\pi+\alpha\))

• \(sin(\pi+\alpha)=-sin\alpha\)
• \(cos(\pi+\alpha)=-cos\alpha\)
• \(tan(\pi+\alpha)=tan\alpha\)
• \(cot(\pi+\alpha)=cot\alpha\)

5) Cung hơn kém \(\dfrac {\pi}{2}\)

• \(cos(\dfrac {\pi}{2}+x)=-sinx\)
• \(sin(\dfrac {\pi}{2}+x)=cosx\)

=> Cách nhớ công thức: cos đối - sin bù - phụ chéo - kém \(pi\) tan, cot.

II. Mở rộng

1. Công thức lượng giác cơ bản

• \(sin^2x+cos^2x=1\)
• \(\dfrac {1}{sin^2x}= 1+ cot^2x\)
• \(\dfrac {1}{cos^2x}= 1+ tan^2x\)
• \(tanx=\dfrac {sinx}{cosx}\)
• \(tanx.cotx=1\)
• \(cosx=\dfrac{cosx}{sinx}\)

2. Công thức cộng

• \(sin(a\pm b)=sina.cosb\pm cosa.sinb\)
• \(cos(a\pm b)=cosa.cosb\mp sina.sinb\)
• \(tan(a\pm b)=\dfrac {tana\pm tanb}{1\mp tana.tanb}\)

3. Công thức nhân đôi

• \(sin2a=2sinacosa\)
• \(cos2a=cos^2a-sin^2a=2cos^2a-1=1-2sin^2a\)
• \(tan2a=\dfrac{2tana}{1-tan^2a}\)

4. Công thức nhân ba

• \(sin3a=3sina-4sin^3a\)
• \(cos3a=4cos^3-3cosa\)
• \(tan3a=\dfrac{3tana-tan^3a}{1-3tan^2a}\)

5. Công thức hạ bậc

• \(sin^2a=\dfrac {1-cos2a}{2}\)
• \(cos^2a=\dfrac {1+cos2a}{2}\)
• \(sin^3a=\dfrac {3sina-sin3a}{4}\)
• \(cos^3a=\dfrac {3cosa+cos3a}{4}\)

6. Công thức biến đổi tổng thành tích

• \(cosa+cosb=2cos\dfrac{a+b}{2}cos\dfrac{a-b}{2}\)
• \(cosa-cosb=-2sin\dfrac{a+b}{2}sin\dfrac{a-b}{2}\)
• \(sina+sinb=2sin\dfrac{a+b}{2}cos\dfrac{a-b}{2}\)
• \(sina-sinb=2cos\dfrac{a+b}{2}sin\dfrac{a-b}{2}\)

7. Công thức biến đổi tích thành tổng

• \(cosa.cosb=\dfrac{1}{2}[cos(a+b)+cos(a-b)]\)
• \(sina.sinb=-\dfrac{1}{2}[cos(a+b)-cos(a-b)]\)
• \(sina.cosb=-\dfrac{1}{2}[sin(a+b)+sin(a-b)]\)

III) Công thức nghiệm của phương trình lượng giác

1. Cơ bản

• \(sinu=sinv\Leftrightarrow \) \(u=v+k2\pi\) hoặc \(u=\pi-v+k2\pi\) 
• \(cosu=cosv\Leftrightarrow u=v+k2\pi\) hoặc \(u=-v+k2\pi\)
• \(tanu=tanv\Leftrightarrow u=v+k\pi\)
• \(cotu=cotv\Leftrightarrow u=v+k\pi\)

2. Trường hợp đặc biệt

• \(sinu=0\Leftrightarrow u=k\pi\)
• \(sinu=1\Leftrightarrow u=\dfrac {\pi}{2}+k2\pi\)
• \(sinu=-1\Leftrightarrow u=-\dfrac {\pi}{2}+k2\pi\)
• \(cosu=0\Leftrightarrow u=\dfrac {\pi}{2}+k\pi\)
• \(cosu=1\Leftrightarrow u=k2\pi\)
• \(cosu=-1\Leftrightarrow u=\pi+k2\pi\)

B. BÀI TẬP VỀ CÔNG THỨC LƯỢNG GIÁC LỚP 10

I. Bài tập tự luận (có lời giải)

Bài 1: Hãy chứng minh \(\dfrac {sin^4a+cos^4a-1}{sin^6+cos^6a-1}=\dfrac{2}{3}\)

=> Lời giải: 

- Ta có: \(sin^4a+cos^4a-1=(sin^2a+cos^2a)^2-2sin^2acoss^2a-1=-2sin^2acos^2a\)

Và: \(sin^6a+cos^6a-1=(sin^2a+cos^2a)(sin^4a-sin^2acos^2a+cos^4a)-1=sin^4a+cos^4a-sin^2acos^2a-1\)

                                    \(=(1-2sin^2acos^2a)-sin^2acos^2a-1=-3sin^2cos^2a\)

- Từ đó suy ra: \(\dfrac {sin^4a+cos^4a-1}{sin^6+cos^6a-1}=\dfrac{-2sin^2acos^2a}{-3sin^2acos^2a}=\dfrac{2}{3}\)

Bài 2: Hãy chứng minh: \(16sin10^0.sin30^0.sin50^0.sin70^0=1\)

=> Lời giải: 

Ta có: \(A=\dfrac{Acos10^0}{cos10^0}=\dfrac{1}{cos10^0}(16sin10^0cos10^0)sin30^0.sin50^0.sin70^0\)

\(\Leftrightarrow A=\dfrac{1}{cos10^0}(8sin20^0)(\dfrac{1}{2})cos40^0.cos20^0\)

\(\Leftrightarrow A=\dfrac{1}{cos10^0}(4sin20^0cos20^0).cos40^0\)

\(\Leftrightarrow A=\dfrac{1}{cos10^0}(2sin40^0).cos40^0\)

\(\Leftrightarrow A=\dfrac{1}{cos10^0}sin80^0=\dfrac{cos10^0}{cos10^0}=1\)

Bài 3: Cho trước tam giác ABC, yêu cầu chứng minh: \(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)

=> Lời giải: 

Ta có: \(\dfrac{A+B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\)

Vậy: \(tan\dfrac{A+B}{2}=cot\dfrac{C}{2}\)

\(\Leftrightarrow \dfrac{tan\dfrac{A}{2}++tan\dfrac{B}{2}}{a-tan\dfrac{A}{2}.tan{B}{2}}=\dfrac{1}{tan\dfrac{C}{2}}\)

\(\Leftrightarrow [tan\dfrac{A}{2}+tan{B}{2}].tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)

\(\Leftrightarrow tan\dfrac{A}{2}tan\dfrac{C}{2}+tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{A}{2}tan\dfrac{B}{2}=1\)

II. Bài tập tự luyện (không lời giải)

Bài 1: Chứng minh: 

a) \(sin^4x+cos^4x=\dfrac{1}{4}(3+cos4x)\)

b) \(sin6x+cos6x=\dfrac{1}{8}(5+3cos4x)\)

c) \(sin^8x+cos^8x=\dfrac{1}{64}(35+28cos4x+cos8x)\)

Bài 2: Chứng minh: \(sin3x.sin^3x+cos3x.cos^3x=cos^32x\) (theo 2 cách khác nhau - nếu có thể)

Bài 3: Chứng minh: \(8sin^318^0+8sin^218^0=1\)

Bài 4: Đặc P = \(sin^250^0+sin^270^0-cos50^0cos70^0\). Tính P?

Gợi ý: P= \(\dfrac{5}{4}\)

Bài 5: Cho trước tam giác ABC. Hãy chứng minh 0 = \(cos2A+cos2B+cos2C+4cossAcosBcosC+1\)

Bài 6: Rút gọn các biểu thức sau:

a) \(\dfrac{tanb}{tanb+cotb}\)

b) \(\dfrac{1-cos^4a-sin^4a}{cos^4a}\)

c) \(sin^3a(1+cota)+cos^3a(1+tana)\)

d) \(sin^4a+cos^2a+sin^2a.cos^2a\)

Xem thêm >>>  Bài tập về Công thức lượng giác lớp 10 SGK

Trên đây là những kiến thức lý thuyết cùng bài tập về công thức lượng giác lớp 10 cần nhớ mà Cunghocvui muốn gửi đến các bạn, mong rằng cách nhớ công thức lượng giác lớp 10 sẽ giúp ích được cho kết quả học tập của các bạn. Nếu thấy hay đừng quên like và share bài viết nhé!