Công thức hàm số lượng giác và các dạng liên quan
Công thức hàm số lượng giác và các dạng liên quan
Bài học hôm nay, chúng ta cùng nhau tìm hiểu về hàm số lượng giác và các vấn đề liên quan, thường gặp trong các bài kiểm tra và bài thi. Bạn đang cảm thấy tò mò lắm đúng không, nào cùng nhau tìm hiểu nhé!
I. Công thức lượng giác

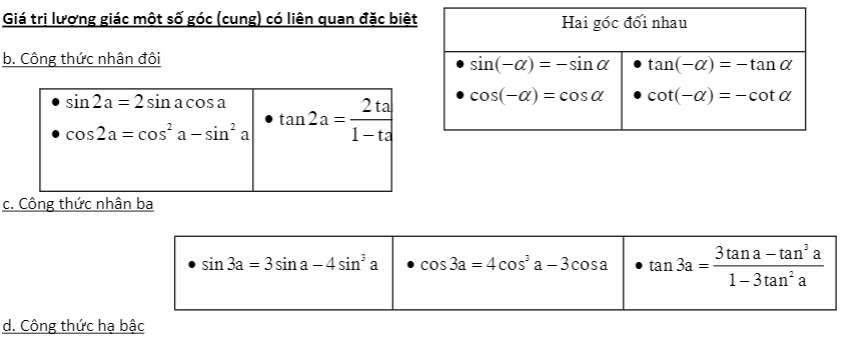
Công thức liên quan:
II. Hàm số lượng giác
1. Giới hạn hàm số lượng giác
Để tìm được giới hạn hàm lượng giác ta tiến hành tìm tập xác định của hàm số lượng giác và áp dụng công thức dưới đây và làm bình thường như hàm số thông thường:
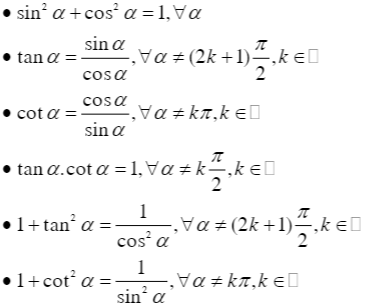

2. Đạo hàm của hàm số lượng giác

3. Tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác
Cho hàm số y = f(x) xác định trên miền D \(\subset\) R.
- Một số thực M được gọi là giá trị lớn nhất của hàm số khi:
\( \left\{ \begin{array}{cc} f(x)\le M,\forall x\in D\\ \exists x_0 \in D \ sao \ cho \ f(x_0)=M \end{array} \right.\)
Ký hiệu: M = max Y
- Một số thực N được gọi là giá trị nhỏ nhất của hàm số khi:
\( \left\{ \begin{array}{cc} f(x)\ge N,\forall x\in D\\ \exists x_0 \in D \ sao \ cho \ f(x_0)=N \end{array} \right.\)
Ký hiệu: N = max Y
Để áp dụng được công thực trên, ta xử lý hàm số lượng giác như sau:
- Biến đổi hàm số lượng giác:
- Dùng tính bị chặn của hàm số sin, cos: \( \left\{ \begin{array}{cc} |sin x|\le 1\\ |cos x|\le 1 \end{array} \right.\)
- Dùng điều kiện cơ bản của các phương trình cơ bản:
Phương trình bậc 2: \(ax^2+bx+c=0 \ có \ nghiệm \ x\in R \) \(\Leftrightarrow \left\{ \begin{array}{cc} \Delta \ge 0\\ a \neq 0 \end{array} \right.\)
Phương trình a sinx + b cosx = c có nghiệm \(x\in R \Leftrightarrow a^2+b^2\ge c^2\).
- Phương pháp sử dụng các hằng đẳng thức cơ bản.
- Phương pháp đạo hàm hàm số.
III. Bài tập hàm số lượng giác
Bài tập trắc nghiệm hàm số lượng giác
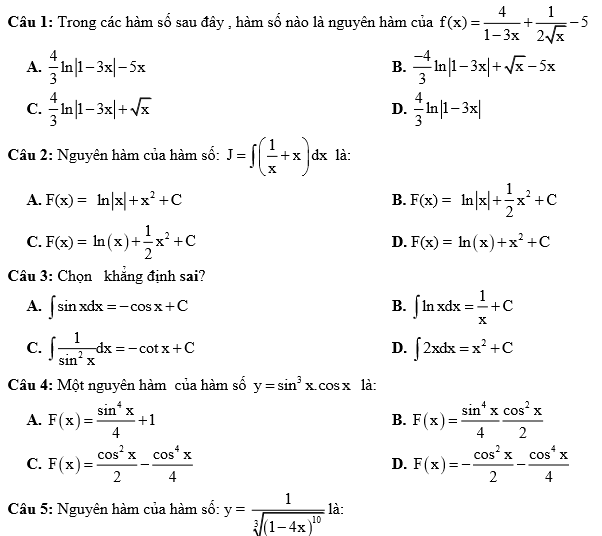
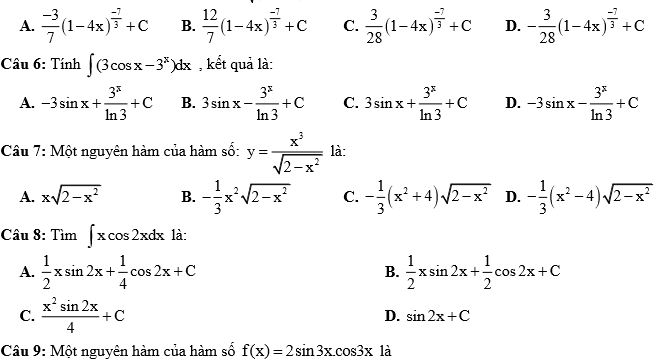
Tham khảo ngay: Giải bài tập hàm số lượng giác lớp 11 sgk
Vừa rồi chúng tôi đã giúp các bạn tổng hợp các dạng bài tập liên quan đến hàm số lượng giác. Mọi thắc mắc và ý kiến đóng góp xin vui lòng để lại dưới comment. Chúng tôi sẽ cố gắng giải đấp cho bạn, cảm ơn sự quan tâm của độc giả!

