Bài tập vận dụng định luật ôm chi tiết nhất

Bài tập vận dụng định luật Ôm là một bài hệ thống lại kiến thức về các dạng mạch điện thuộc chương I Vật lý 9. Cunghocvui xin gửi tới các bạn bài tham khảo tổng hợp lý thuyết và các dạng các dạng bài tập vận dụng định luật Ôm. Hy vọng với bài viết bài 6 bài tập vận dụng định luật Ôm, các bạn sẽ hiểu sâu và áp dụng định luật Ôm vào các bài tập!

A. Một số kiến thức cần phải nhớ để áp dụng vào bài tập vận dụng định luật Ôm

1. Với đoạn mạch được mắc có dạng nối tiếp

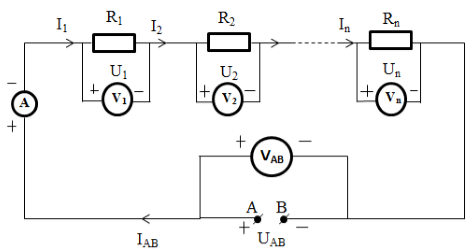
Trong đoạn mạch được mắc dạng nối tiếp, ta có một số đặc điểm về điện trở, hiệu điện thế và cường độ của dòng điện như sau:

- Với cường độ dòng điện: Với các đoạn mạch được mắc nối tiếp thì cường độ dòng điện mạch chính đúng bằng các cường độ mà dòng điện chạy qua các mạch rẽ.

\(I_{AB}=I_{1}=I_{2}=I_{n}\)

- Với hiệu điện thế: Với các đoạn mạch được mắc nối tiếp thì tổng hiệu điện thế ở vị trí các mạch rẽ bằng giá trị hiệu điện thế ở vị trí hai đầu đoạn mạch.

\(U_{AB}=U_{1}+U_{2}+...+U_{n}\)

- Với điện trở tương đương: Với các đoạn mạch được mắc nối tiếp thì điện trở tương đương bằng tổng các điện trở thành phần có trong đoạn mạch.

\(R_{AB}=R_{1}+R_{2}+...R_{n}\)

2. Với đoạn mạch được mắc dạng song song 

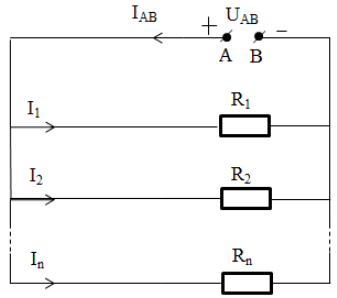
Trong đoạn mạch được mắc dạng song song, ta có một số đặc điểm về điện trở, hiệu điện thế và cường độ của dòng điện như sau:

- Với cường độ dòng điện: Với các đoạn mạch được mắc dạng song song thì cường độ dòng điện mạch bằng tổng các cường độ mà dòng điện chạy qua các mạch rẽ.

\(I_{AB}=I_{1}+I_{2}+...+I_{n}\)

- Với hiệu điện thế: Với các đoạn mạch được mắc dạng song song thì hiệu điện thế ở vị trí giữa hai đầu đoạn mạch đúng bằng các hiệu điện thế giữa các mạch rẽ.

\(U_{AB}=U_{1}=U_{2}=U_{n}\)

- Với điện trở tương đương: Với các đoạn mạch được mắc dạng song song thì nghịch đảo điện trở tương đương bằng tổng các nghịch đảo điện trở thành phần có trong đoạn mạch.

\(\dfrac{1}{AB}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+...+\dfrac{1}{R_{n}}\)

B. Các dạng bài tập vận dụng định luật Ôm

1. Dạng 1: Dạng mạch hỗn hợp giữa đoạn mạch được mắc kết hợp giữa hai dạng là song song và nối tiếp

a, Cách giải bài tập vận dụng định luật Ôm

Trong đoạn mạch hỗn hợp, ta chia nhỏ đoạn mạch thành nhiều phần sao cho trong mỗi phần của đoạn mạch chỉ có 1 cách mắc. Trên mỗi đoạn mạch thành phần, áp dụng định luật Ôm để tìm các giá trị về điện trở, cường độ của dòng điện và hiệu điện thế.

b, Một số bài tập vận dụng định luật Ôm

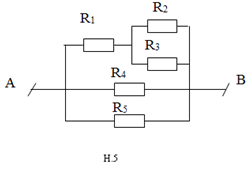
Bài 1: Một đoạn mạch được cho dưới dạng hình vẽ (hình 5) được cho với các dữ liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\), \(R_{3}\), \(R_{4}\) và \(R_{5}\) lần lượt nhận các giá trị là \(10\Omega\), \(3\Omega\), \(6\Omega\), \(6\Omega\) và \(4\Omega\). Biết rằng mạch chính có dòng điện chạy qua với một cường độ là 6A. Hỏi qua mỗi điện trở thành phần, dòng điện chạy qua với một cường độ là bao nhiêu?

Hướng dẫn giải bài tập bài 1 dạng mạch hỗn hợp: 

Điện trở toàn mạch có dạng mắc là [\(R_{1}\) nt (\(R_{2}\) // \(R_{3}\))] // \(R_{4}\) // \(R_{5}\)

- Với nhánh 1 bao gồm đoạn mạch \(R_{1}\) nt (\(R_{2}\) // \(R_{3}\))

Ta có điện trở toàn mạch được tính bằng: \(R_{123}\) = \(R_{1}\) + \(\dfrac{R_{2}.R_{3}}{R_{2}+R_{3}}\) = \(10\) + \(\dfrac{3.6}{3+6}\) = \(12\Omega\)

- Với toàn mạch AB ta có:

\(\dfrac{1}{AB}=\dfrac{1}{R_{123}}+\dfrac{1}{R_{4}}+\dfrac{1}{R_{5}}\) = \(\dfrac{1}{12}+\dfrac{1}{6}+\dfrac{1}{4}\) = \(\dfrac{1}{2}\) => \(R=2\Omega\)

Vậy hiệu điện thế ở vị trí hai đầu đoạn mạch của mạch hỗn hợp AB là: 

\(U_{AB}=I.R_{AB}\) = \(6.2\) = \(6.2\)

Với điện trở \(R_{1}\), dòng điện chạy qua với cường độ là:

\(I_{1}=\dfrac{U_{AB}}{R_{123}}\) = \(\dfrac{2}{3}A\)

Vì \(R_{1}\) nt (\(R_{2}\) // \(R_{3}\)) => \(I_{23}=I_{1}\)

Ta có với đoạn mạch gồm hai điện trở là \(R_{2}\) và \(R_{3}\) sẽ có hiệu điện thế là: \(U_{23}=I_{23}.R_{23}\) = \(1.2\) = \(2V\)

Trong đoạn mạch \(R_{2}\) // \(R_{3}\) ta có dòng điện chạy qua từng điện trở có cường độ là:

\(I_{12}=\dfrac{U_{23}}{R_{2}}\) = \(\dfrac{2}{3}A\), \(I_{3}=\dfrac{U_{23}}{R_{3}}\) = \(\dfrac{1}{3}A\)

Với điện trở \(R_{4}\) ta có dòng điện chạy qua từng điện trở có cường độ là:

\(I_{4}=\dfrac{U_{4}}{R_{4}}\) = \(\dfrac{12}{6}A\) = \(2A\)

Với điện trở \(R_{5}\) ta có dòng điện chạy qua từng điện trở có cường độ là:

\(I_{5}=\dfrac{U_{AB}}{R_{5}}\) = \(\dfrac{12}{4}A\) = \(3A\)

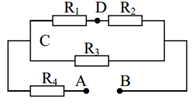
Bài 2: Một đoạn mạch được cho dưới dạng hình vẽ (hình dưới) được cho với các dữ liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\), \(R_{3}\), \(R_{4}\) với các giá trị được nhận lần lượt là \(10\Omega\), \(20\Omega\), \(20\Omega\), \(8\Omega\). Biết rằng mạch chính có hiệu điện thế ở vị trí giữa hai đầu đoạn mạch là 12V. Hỏi:

a, Điện trở của toàn mạch điện hỗn hợp là bao nhiêu?

b, Khi đi qua các điện trở thì hiệu điện thế và dòng điện có cường độ là bao nhiêu?

Hướng dẫn giải bài tập bài 2 dạng mạch hỗn hợp:

Điện trở toàn mạch có dạng mắc là [(\(R_{1}\) nt \(R_{2}\)) // \(R_{3}\))] nt \(R_{4}\)

a, Với nhánh 1 bao gồm đoạn mạch (\(R_{1}\) nt \(R_{2}\)) // \(R_{3}\)

\(R_{123}=\dfrac{(R_{1}+R_{2}).R_{3}}{R_{1}+R_{2}+R_{3}}\) = \(\dfrac{(10+20).30}{10+20+30}\) = \(12\Omega\)

Vì [(\(R_{1}\) nt \(R_{2}\)) // \(R_{3}\))] nt \(R_{4}\) => \(R_{AB}\) = \(R_{123}\) + \(R_{4}\) = \(12+8\) = \(20\Omega\)

b, Vì [(\(R_{1}\) nt \(R_{2}\)) // \(R_{3}\))] nt \(R_{4}\) nên ta có: \(I_{123}\) = \(I_{4}\) = \(\dfrac{U}{R_{AB}}\) = \(\dfrac{12}{20}\) = \(0,6A\)

Vậy khi đi qua điện trở \(R_{4}\) thì hiệu điện thế sẽ bằng: \(U_{4}\) = \(I_{4}\).\(R_{4}\) = \(0,6.8\) = \(4,8V\)

Vì (\(R_{1}\) nt \(R_{2}\)) // \(R_{3}\) => \(U_{123}\) = \(U_{12}\) = \(U_{3}\) = \(U_{AB}\) - \(U_{4}\) = \(12 -4,8\) = \(7,2V\)

Với điện trở \(R_{3}\) ta có dòng điện chạy qua từng điện trở có cường độ là:

\(I_{3}=\dfrac{U_{3}}{R_{3}}\) = \(\dfrac{7,2}{20}\) = \(0,36A\)

Với điện trở \(R_{1}\) và \(R_{2}\) ta có dòng điện chạy qua từng điện trở có cường độ là:

\(I_{12}=I_{1}=I_{2}=\dfrac{U_{12}}{R_{1}+R_{2}}\) = \(\dfrac{7,2}{10+20}\) = \(0,24A\)

Vậy khi đi qua điện trở \(R_{1}\) thì hiệu điện thế sẽ bằng: \(U_{1}\) = \(I_{1}\).\(R_{1}\) = \(0,24.10\) = \(2,4V\)

Vậy khi đi qua điện trở \(R_{2}\) thì hiệu điện thế sẽ bằng: \(U_{2}\) = \(U_{12}\) -  \(U_{1}\) = \(7,2-2.4\) = \(4,8V\)

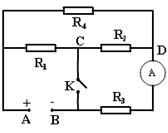
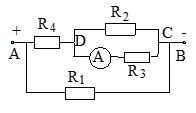
Bài 3: Với một mạch điện như hình vẽ (phía dưới) được cho với các dữ liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\), \(R_{3}\), \(R_{4}\) với các giá trị được nhận lần lượt là \(8\Omega\), \(4\Omega\), \(4\Omega\), \(6\Omega\). Biết rằng mạch chính có hiệu điện thế ở vị trí giữa hai đầu đoạn mạch là 6V. Giả sử ampe kế, dây dẫn và khóa K có điện trở là không đáng kể thì điện trở của toàn mạch AB và ampe kế có chỉ số là bao nhiêu khi khóa K trong tình trạng đóng và mở?

Hướng dẫn giải bài tập bài 3:

a, Trường hợp 1: Khi khóa K trong tình trạng mở thì sơ đồ mạch sẽ được chuyển sang dạng như sau:

Đoạn mạch có dạng [(\(R_{1}\)nt \(R_{2}\)) // \(R_{4}\)] nt \(R_{3}\)

Với nhánh 1 bao gồm đoạn mạch [(\(R_{1}\)nt \(R_{2}\)) // \(R_{4}\)]

\(R_{124}=\dfrac{(R_{1}+R_{2}).R_{4}}{R_{1}+R_{2}+R_{4}}\) = \(\dfrac{(8+4).6}{8+4+6}\) = \(4\Omega\)

Vì [(\(R_{1}\)nt \(R_{2}\)) // \(R_{4}\)] nt \(R_{3}\) => \(R_{AB}=R_{124} +R_{3}\) = \(4+4=8\Omega\)

\(I_{A}=\dfrac{U_{AB}}{R_{AB}}\) = \(\dfrac{6}{8}\) = \(0,75A\)

b, Trường hợp 2: Khi khóa K trong tình trạng đóng thì sơ đồ mạch sẽ được chuyển sang dạng như sau:

Vì \(R_{2}\) = \(R_{3}\) => \(R_{DC}\) = \(\dfrac{R_{3}}{2}\) = \(2\Omega\)

\(R_{AB}=\dfrac{(R_{4}+R_{DC}).R_{1}}{R_{1}+R_{DC}+R_{4}}\) = \(4\Omega\)

\(U_{AB}=\dfrac{R_{DC}}{R_{4}+R_{DC}}.U_{AB}\) = \(1,5V\)

Với điện trở \(R_{3}\) ta có dòng điện chạy qua từng điện trở có cường độ là:

\(I_{3}=I_{A}\) = \(\dfrac{U_{DC}}{R_{3}}\) = \(\dfrac{1,5}{4}\) = \(0,375(A)\)

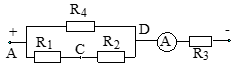
Bài 4: Một đoạn mạch được cho dưới dạng hình vẽ (hình dưới) được cho với các dữ liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\), \(R_{3}\), \(R_{4}\) và \(R_{5}\) với các giá trị được nhận lần lượt là \(10\Omega\), \(30\Omega\), \(10\Omega\), \(30\Omega\) và \(50\Omega\). Biết rằng mạch chính có hiệu điện thế ở vị trí giữa hai đầu đoạn mạch là 30V. Sáng tỏ rằng qua điện trở \(R_{5}\) thì dòng điện có cường độ bằng 0?

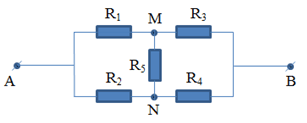
Hướng dẫn giải bài tập bài 5 dạng đoạn mạch hỗn hợp:

Theo sơ đồ của mạch điện ta có:

\(U_{MN}=U_{AN}+U_{MN}\) => \(U_{MN}=U_{AM}-U_{AN}​​\) = \(U_{1}-U_{2}​​\)

Mà ta lại có: \(U_{1}+U_{3}\) = \(U_{2}+U_{4}\) = \(U_{AB}\) 

=> \(U_{1}\) = \(U_{2}\) = \(U_{3}\) = \(U_{4}\) = \(\dfrac{1}{2}\)\(U_{AB}\)  => \(U_{1}-U_{2}​​\) = \(0\)

Vậy qua điện trở \(R_{5}\) thì dòng điện có cường độ bằng 0

2.  Một số câu hỏi trắc nghiệm bài 6 bài tập vận dụng định luật Ôm 

Câu 1: Với một mạch điện được cho bởi hình vẽ với các số liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\), \(R_{3}\) với các giá trị được nhận lần lượt là \(9\Omega\), \(15\Omega\), \(10\Omega\). Biết rằng điện trở \(R_{3}\) có dòng điện chạy qua với một cường độ là 0,3A. Vậy ở vị trí giữa hai đầu mạch điện AB thì hiệu điện thế sẽ nhận giá trị là: 

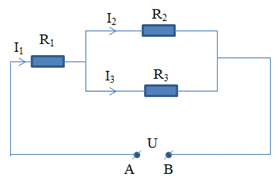
\(A. 6,5V\)

\(B. 2,5V\)

\(C. 7,5V\)

\(D. 5,5V\)

Câu 2: Với một mạch điện được cho bởi hình vẽ với các số liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\) với các giá trị được nhận lần lượt là \(7\Omega\), \(12\Omega\). Biết rằng trên toàn mạch điện trở nhận giá trị \(R_{AB}=10\Omega\). Vậy ở vị trí \(R_{x}\) sẽ nhận giá trị điện trở bằng bao nhiêu?

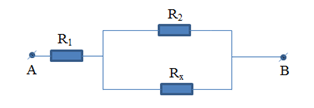
\(A. 9\Omega\)

\(B. 5\Omega\)

\(C. 15\Omega\)

\(D. 4\Omega\)

Câu 3: Với một mạch điện được cho bởi hình vẽ với các số liệu như sau: Các điện trở \(R_{1}\), \(R_{2}\), \(R_{3}\)  \(14\Omega\), \(8\Omega\), \(24\Omega\). Trên điện trở \(R_{1}\) có một dòng điện với cường độ là 0,4A chạy qua. Vậy trên điện trở \(R_{2}\) và \(R_{3}\), cường độ của dòng điện chạy qua theo thứ tự lần lượt là bao nhiêu?

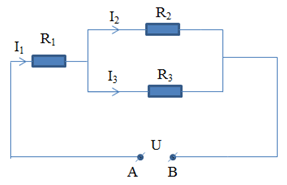
A. 0,1A và 0,3A

B. 3A và 1A

C. 0,1A và 0,1A

D. 0,3A và 0,1A

Câu hỏi	1	2	3
Đáp án	C	D	D

Tham khảo thêm >>> Giải bài tập vận dụng định luật Ôm lớp 9 (làm anchor text)

Cunghocvui đã đem đến cho các bạn bài tổng hợp lý thuyết và các dạng bài tập tự luận cũng như tự luận đầy đủ nhất về định luật Ôm thông qua bài viết bài tập vận dụng định luật ôm. Nếu có đóng góp hay thắc mắc gì về bài viết bài 6 bài tập vận dụng định luật Ôm, các bạn hãy để lại comment dưới phần bình luận nhé!