30 bài tập trắc nghiệm đường tiệm cận của đồ thị hàm số mức độ vận dụng, vận dụng cao

Câu 1 : Cho hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\). Tìm tất cả các giá trị của \(m\) sao cho đồ thị hàm số có đúng hai đường tiệm cận đứng.

A \(m \in \left[ {6;8} \right)\)

B \(m \in \left( {6;8} \right)\)

C \(m \in \left[ {12;16} \right)\)

D \(m \in \left( {0;16} \right)\)

Câu 2 : Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 100;100} \right]\) để đồ thị hàm số \(y = \dfrac{1}{{\left( {x - m} \right)\sqrt {2x - {x^2}} }}\) có đúng 2 tiệm cận?

A \(200\)

B \(2\)

C \(199\)

D \(0\)

Câu 3 : Biết đồ thị hàm số \(y = \dfrac{{\sqrt {x + 3} + ax + b}}{{{{\left( {x - 1} \right)}^2}}}\) không có đường tiệm cận đứng nào. Tính \(T = a - 3b.\)

A \(T = 6.\)

B \(T = 4.\)

C \(T = 3.\)

D \(T = 5.\)

Câu 4 : Đồ thị trong hình bên là của hàm số \(y = \dfrac{{ax + b}}{{x + c}}\)(với \(a,b,c \in \mathbb{R}\)). Khi đó tổng \(a + b + c\) bằng

A \( - 1.\)

B \(1\).

C \(2\).

D \(0\).

Câu 5 : Cho hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\). Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

A \(3\)

B \(2\)

C \(5\)

D \(4\)

Câu 6 : Gọi \(S\) là tập hợp các giá trị nguyên \(m\) để đồ thị hàm số \(y = \dfrac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là:

A Vô số

B \(13\)

C \(12\)

D \(14\)

Câu 7 : Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = m.\) Có bao nhiêu giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có duy nhất một tiệm cận ngang.

A \(1.\)

B \(0.\)

C \(2.\)

D Vô số.

Câu 8 : Cho hàm số \(f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), có bảng biến thiên như sau:

A \(4\)

B \(3\)

C \(2\)

D \(1\)

Câu 9 : Cho hàm số \(y = \dfrac{{3x + 1}}{{x - 4}}\) có đồ thị \(\left( C \right)\), với mọi điểm \(M\) thuộc \(\left( C \right)\) thì tích các khoảng cách từ \(M\) tới 2 đường tiệm cận của \(\left( C \right)\) bằng:

A \(11\)

B \(12\)

C \(14\)

D \(13\)

Câu 10 : Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x\sqrt {2 - {x^2}} }}{{{x^2} + x - 2}}\) là

A \(1\)

B \(2\)

C \(4\)

D \(3\)

Câu 11 : Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 10;10} \right]\) để đồ thị hàm số \(y = \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}}\) có ba đường tiệm cận?

A \(7\)

B \(8\)

C \(10\)

D \(6\)

Câu 12 : Cho hàm số \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\,\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:

A \(2.\)

B

\(3.\)

C \(1.\)

D \(0.\)

Câu 13 : Số giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\) có 3 tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) là

A \(0\)

B \(3\)

C \(2\)

D \(1\)

Câu 14 : Cho hàm số \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}}\). Số giá trị thực của \(m\) để đồ thị hàm số có đúng hai đường tiệm cận ?

A \(2\).

B \(3\).

C \(0\).

D \(1\).

Câu 15 : Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên.

A \(4\)

B \(3\)

C \(5\)

D \(2\)

Câu 16 : Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = \dfrac{{x - 1}}{{{x^2} + 2mx - m + 2}}\) có đúng hai đường tiệm cận. Tổng tất cả các phần tử của tập \(S\) bằng:

A \( - 4\)

B \( - 2\)

C \( - 5\)

D \( - 1\)

Câu 17 : Cho hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\,\,\left( C \right)\). Biết rằng \({M_1}\left( {{x_1};{y_1}} \right)\) và \({M_2}\left( {{x_2};{y_2}} \right)\) là hai điểm trên đồ thị \(\left( C \right)\) có tổng khoản cách đến hai tiệm cận của \(\left( C \right)\) nhỏ nhất. Tính giá trị \(P = {x_1}{x_2} + {y_1}{y_2}\).

A \(0\)

B \( - 2\)

C \(1\)

D \( - 1\)

Câu 18 : Cho hàm đa thức bậc ba \(y = f\left( x \right)\) có đò thị như hình vẽ

A

\(1\)

B

\(2\)

C \(3\)

D \(4\)

Câu 19 : Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có đồ thị như hình dưới đây.

A \(2016.\)

B \(4034.\)

C \(4036.\)

D \(2017.\)

Câu 20 : Có bao nhiêu giá trị nguyên của \(m\) để đồ thị hàm số \(y = \frac{{x - 2}}{{{x^2} - 3mx + m}}\) có đúng một tiệm cận đứng?

A \(1.\)

B \(2.\)

C \(3.\)

D \(4.\)

Câu 21 : Xác định số đường đường tiệm cận của đồ thị hàm số \(y = \dfrac{{\sqrt {x + 4} - 2}}{{{x^2} + 5x}}\).

A \(3\)

B \(2\)

C \(0\)

D \(1\)

Câu 22 : Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{\left( {\sqrt {x + 1} - 2} \right)\sin x}}{{{x^3} - {x^2} - 6x}}\) là

A \(2.\)

B \(0.\)

C \(3.\)

D \(1.\)

Câu 23 : Tồn tại bao nhiêu giá trị nguyên của tham số \(m\) trong đoạn \(\left[ -2017;2017 \right]\) sao cho đồ thị hàm số \(y=\frac{x-2}{\left( {{x}^{2}}-4mx+4 \right)\left( m{{x}^{2}}-2x+4 \right)}\) có đúng một đường tiệm cận.

A \(1\)

B \(2017\)

C \(4034\)

D \(0\)

Câu 24 : Cho (C) là đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\). Tìm các điểm trên (C) sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất:

A

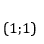
B \(\left( {2 + \sqrt 3 ;1 + \sqrt 3 } \right)\) và \(\left( {2 - \sqrt 3 ;1 - \sqrt 3 } \right)\)

C \(\left( {1 - \sqrt 3 ;1 - \sqrt 3 } \right)\)

D \(\left( {1 + \sqrt 3 ;1 + \sqrt 3 } \right)\)

Câu 25 : Đồ thị hàm số nào sau đây không có đường tiệm cận?

A \(y = x + 2 - \dfrac{1}{{x + 3}}\)

B \(y = \sin x\)

C \(y = \dfrac{{x - 2}}{{3x + 2}}\)

D \(y = \dfrac{x}{{2{x^2} - 1}}\)

Câu 26 : Cho hai hàm số \(y = \dfrac{{2x - 1}}{{{m^2} - 8 - x}}\) và \(y = \dfrac{{5 - 2x}}{{x + 4}}\). Tập hợp các giá trị của tham số \(m\) để hai đường tiệm cận đứng của hai đồ thị hàm số trên trùng nhau là:

A {-2,2}

B {-1;2}

C {0}

D {2;3}

Câu 27 : Gọi \(a;\,b;\,c\) lần lượt là số các đường tiệm cận của đồ thị hàm số sau: \(y = \dfrac{{1 - 2x}}{{x - 4}};\)\(y = \dfrac{{ - x - 2}}{{{x^2} - 3}}\) và \(y = \dfrac{{25}}{{2{x^2} - 3x + 4}}\). Bất đẳng thức nào sau đây đúng?

A \(a < b < c\)

B \(b < a < c\)

C \(c < a < b\)

D \(c < b < a\)

30 bài tập trắc nghiệm đường tiệm cận của đồ thị h...