100 câu trắc nghiệm Tích vô hướng của hai vectơ nâ...
- Câu 1 : Cho tam giác ABC thoả mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng ?
A. cosB + cosC = 2cos A
B. sinB + sinC = 2sinA
C. sin C = cosA + sin B
D. sinB + cosA = cosC
- Câu 2 : Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Câu nào sau đây sai?
A.
B.
C.
D.
- Câu 3 : Cho 2 vec tơ . Biểu thức sai là:
A.
B.
C.
D.
- Câu 4 : Cho tam giác ABC. Đẳng thức nào sai ?
A. sin( A + B - 2C) = sin3C
B.
C. sin( A + B) = sinC
D.
- Câu 5 : Cho A(2; 5); B(1; 3) và C(5; -1). Tìm tọa độ điểm K sao cho
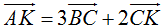
A. (-4; -4).
B. (-4; 5).
C. (5; -4).
D. (-5; -4).
- Câu 6 : Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC. Tính
A.
B. -
C.
D. -
- Câu 7 : Cho tam giác ABC là tam giác đều. Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
- Câu 8 : Tam giác ABC có a = 6; ; c = 2; gọi M là điểm trên cạnh BC sao cho BM = 3 . Độ dài đoạn AM bằng bao nhiêu ?
A. 5
B. 9
C. 3
D. 6
- Câu 9 : Tính giá trị biểu thức P = cos300.cos600 – sin300.sin600
A.
B. 2
C. 1
D. 0
- Câu 10 : Tính giá trị biểu thức P = sin300.cos600 + cos300.sin600
A. 1
B. 0
C. 2
D.
- Câu 11 : Cho tam giác ABC vuông tại A có AC = 12; M là trung điểm AC. Tính
A. 12
B. -36
C. 36
D. -72
- Câu 12 : Cho tứ giác lồi ABCD có AD = 6cm. Đặt . Tính
A. 18
B. 32
C. 36
D. 40
- Câu 13 : Cho tam giác ABC có cạnh BC = 6cm và đường cao AH; H ở trên cạnh BC sao cho BH = 2HC. Tính
A. -24
B. 24
C. 16
D. -12
- Câu 14 : Cho tam giác đều ABC cạnh a, với các đường cao AH và BK vẽ HI vuông góc với AC. Câu nào sau đây đúng?
A.
B.
C.
D. Cả ba câu trên.
- Câu 15 : Cho tam giác đều ABC cạnh a; với các đường cao AH; BK vẽ HI ⊥ AC. Câu nào sau đây đúng?
A.
B .
C.
D.
- Câu 16 : Cho 2 vectơ có . Tính
C. 21
D. 61
- Câu 17 : Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.
A. -3a2
B. -2a2
C. -4 a2/3
D. 2a2
- Câu 18 : Cho hai điểm A( -3;2) : B(4;3). Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M
A. M(7; 0)
B. M(5; 0)
C. M(3; 0)
D. tất cả sai
- Câu 19 : Cho 2 vectơ đơn vị thỏa mãn . Hãy xác định
A. 5
B. -3
C. -5
D. -7
- Câu 20 : Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau:
A. a2
B. –a2
C. 2a2
D. Đáp án khác
- Câu 21 : Cho hai vecto . Biết
A.
B.
C.
D.
- Câu 22 : Cho hai điểm B; C phân biệt. Tập hợp những điểm M thỏa mãn là :
A. Đường tròn đường kính BC.
B. Đường tròn (B; BC).
C. Đường tròn (C: BC).
D. Một đường khác.
- Câu 23 : Cho ba điểm A: B: C phân biệt. Tập hợp những điểm M mà là :
A. Đường tròn đường kính AB.
B.Đường thẳng đi qua A và vuông góc với BC.
C. Đường thẳng đi qua B và vuông góc với AC.
D. Đường thẳng đi qua C và vuông góc với AB.
- Câu 24 : Cho hai điểm A(2; 2); B( 5; -2) . Tìm M trên tia Ox sao cho
A. M(1; 4)
B. (0; 6)
C. M(1;0) hoặc M(6; 0)
D. M(0;1)
- Câu 25 : Trong mặt phẳng tọa độ Oxy cho hai vectơ . Tìm k để vectơ vuông góc với vectơ
A. k = 2
B. k = 8
C. k = -4
D. k = 4
- Câu 26 : Cho tam giác ABC có BC = a; CA = b; AB = c. Tính
A. ½.( c2 + b2 - a2)
B. c2 + b2 - a2
C. a2 - b2 - c2
D. a2 + b2 + c2
- Câu 27 : Cho tam giác ABC có BC = a; CA = b; AB = c. M là trung điểm của BC, D là chân đường phân giác trong góc A. Tính
A.
B.
C.
D.
- Câu 28 : Cho các vectơ có độ dài bằng 1 và thoả mãn điều kiện . Tính cos
A. 1
B. 0
C. 0,5
D. Tất cả sai
- Câu 29 : Cho các véctơ có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ
A. -1/2
B. -1/4
C. -1/6
D. 0
- Câu 30 : Giá trị của E = sin360.cos60 - sin1260.cos840 là
A. 0,5
C. 1
D. -1
- Câu 31 : Giá trị của biểu thức A = sin2410 + sin2450 + sin2490 + sin2450 là
A. 3.
B. 4.
C. 1.
D. 2.
- Câu 32 : Cho biết cosα = -2/3 . Tính giá trị của biểu thức ??
A.
B.
C.
D. -
- Câu 33 : Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB = CD = 2a; .
A. 300
B. 450
C. 600
D. 900
- Câu 34 : Tính A = sin220 + sin240 + sin2 60 +… + sin2840 + sin2860 + sin2880.
A. 20
B. 22
C. 24
D. 23
- Câu 35 : Biết sina+ cosa = . Hỏi giá trị của sin4a + cos4a bằng bao nhiêu?
A. 1
B. 0,5
C. -1
D. 0
- Câu 36 : Biểu thức A = 3(sin4x + cos4x) - 2 (sin6x + cos6x) có giá trị bằng:
A. 1
B. 2
C. -1
D. 0
- Câu 37 : Biểu thức: A = cos4x + cos2x sin2x + sin2x có giá trị bằng
A. 1
B. 2
C. 3
D. 4
- Câu 38 : Biểu thức B = sin2x.tan2x – tan2x + sin2 x có giá trị bằng
A. -2
B. -1
C. 0
D. 1
- Câu 39 : Cho cotα = 1/3. Giá trị của biểu thức
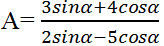 là:
là: A. -11
B. 11
C. 12
D. 13
- Câu 40 : Cho biết cosα = -2/3. Giá trị của biểu thức bằng bao nhiêu?
A .
B.
C. -
D.
- Câu 41 : Cho tanα + cotα = m. Tìm m để tan2α + cot2α = 7.
A. m = 3
B. m = 6
C. m = -3
D. m = ± 3
- Câu 42 : Biểu thức (cota + tana)2 bằng
A.
B. cot2a + tan2a.
C .
D. cot2a.tan2a + 2.
- Câu 43 : Đơn giản biểu thức ta được
A. sinx
B.
C.
D. tanx
- Câu 44 : Rút gọn biểu thức sau
A. A = 1
B. A = -1
C. A = -2
D. A = 2
- Câu 45 : Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?
A.
B.
C.
D.
- Câu 46 : Trong mặt phẳng tọa độ Oxy cho các điểm A(1;2); B(-2; -4) và C(0;1); D(-1; 3/2). Mệnh đề nào sau đây đúng ?
A.
B.
C.
D.
- Câu 47 : Cho . Giá trị của m để 2 vecto cùng phương là:
A. -6.
B.
C. 8.
D.
- Câu 48 : Cho các điểm A(1;1) ; B( 2;4) và C(10; -2) . Góc BAC bằng bao nhiêu độ?
A. 900
B. 450
C. 1200
D. 300
- Câu 49 : Gọi
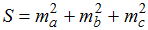 là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng ?
là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng ? A. S = ¾.( a2 + b2 + c2).
B. S = a2
C. S = 3/2.( a2 + b2 + c2).
D. S = 3( a2 + b2 + c2).
- Câu 50 : Cho tam giác ABC có a2 + b2 - c2 > 0. Khi đó :
A. Góc C > 900.
B. Góc C < 900.
C. Góc C = 900.
D. Không thể kết luận được gì về góc C.
- Câu 51 : Một tam giác có ba cạnh là 52; 56; 60. Bán kính đường tròn ngoại tiếp là:
A. 32,5
B. 32
C. 36
D. Đáp án khác
- Câu 52 : Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một cái ao. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78024’ . Biết CB = 120m và CA = 250 m. Khoảng cách AB bằng bao nhiêu ?
A. 198
B. 255
C. 156
D. 237
- Câu 53 : Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 600. Tàu thứ nhất chạy với tốc độ 30 km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?
A. 13
B.
C.
D. 15
- Câu 54 : Tam giác ABC có BC = a; CA = b và AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S
B. 3S
C. 4S
D. 6S
- Câu 55 : Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
A. 600
B. 900
C. 1500
D. 1200
- Câu 56 : Cho tam giác ABC thoả mãn . Khi đó :
A. A = 300
B. A = 900
C. A = 600
D. A = 1200
- Câu 57 : Tam giác ABC có a = 16,8; . Cạnh c gần với giá trị nào nhất?
A. 14
B. 16
C. 19
D. 20
- Câu 58 : Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là
A.
B. 6.
C.
D.
- Câu 59 : Cho tam giác ABC có A(5;3); B(2;-1) và C(-1; 5). Tìm tọa độ trực tâm tam giác ABC.
A. H(1;2)
B. (2;3)
C. (3;2)
D. (1;3)
- Câu 60 : Cho tam giác ABC có A(5;3) : B(2;-1) và C(-1; 5). Tính tọa độ chân đường cao vẽ từ A.
A. (1;2)
B. ( 1;1)
C. (1;-1)
D. (-2; 1)
- Câu 61 : Cho tam giác ABC có A(5;3) : B(2;-1) và C(-1; 5). Tính diện tích tam giác ABC.
A. 5
B. 10
C. 15
D. 20
- Câu 62 : Cho ba điểm A(6; 3) ; B(-3; 6) và C(1;-2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
A. (1; 2)
B. (2; 4)
C. ( 1; -3)
D. (1; 3)
- Câu 63 : Biết A(1;-1) và B(3;0) là hai đỉnh của hình vuông ABCD. Tìm tọa độ các đỉnh C ?
A. (4;2)
B. (2;2)
C. (4; -2)
D. Cả B và C đúng
- Câu 64 : Trong mặt phẳng tọa độ cho ba điểm A(1; 4) ; B( -2; -2) và C( 4; 2). Xác định tọa độ điểm M sao cho tổng MA2 + 2MB2 + 3MC2 nhỏ nhất.
A. (1;1)
B. (0,5; 1)
C. (1,5; 0)
D. (1,5; 1)
- Câu 65 : Cho hình chữ nhật ABCD biết AD = 1 . Giả sử E là trung điểm AB và thỏa mãn .Tính độ dài cạnh AB.
A. 1
B. 2
C .
D.
- Câu 66 : Cho tam giác ABC vuông tại B có AB=1. Trên tia đối của CA lấy điểm D sao cho CD = AB. Giả sử góc CBD bằng 300. Tính AC.
A. 1
B.
D. Đáp án khác
- Câu 67 : Cho tam giác ABC thỏa mãn sin2A = sinB. sinC. Hỏi mệnh đề nào đúng.
A. a2 = bc
B. cosA ≥ ½
C. Cả A và B sai
D. Cả A và B đúng
- Câu 68 : Cho tam giác ABC Và G là trọng tâm tam giác.Nếu tam giác GBC vuông tại G thì khẳng định nào sau đây đúng?
A. a2 = b2 + 2c2
B. 3b2 = a2 + c2
C. 5a2 = b2 + c2
D. Tất cả sai
- Câu 69 : Cho tam giác ABC thỏa mãn a4 = b4 + c4. Tìm khẳng định đúng.
A. Tam giác ABC nhọn
B. Tam giác ABC là tam giác tù
C. Tam giác ABC là tam giác vuông
D. Tam giác ABC là tam giác cân
- Câu 70 : Cho tam giác ABC thỏa mãn: a.sinA + b.sinB + c.sinC = ha + hb + hc. Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân
C. Tam giác ABC là tam giác vuông
D. tam giác ABC là tam giác tù
- Câu 71 : Cho tam giác ABC thỏa mãn: Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân tại C
C. Tam giác ABC là tam giác cân tại A
D. tam giác ABC là tam giác nhọn
- Câu 72 : Cho tam giác ABC. Biết các cạnh a, b, c đôi một khác nhau thoả mãn hệ thức: b(b2 - a2) = c(c2 - a2). Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân
C. Tam giác ABC là tam giác tù
D. tam giác ABC là tam giác nhọn
- Câu 73 : Cho tam giác ABC thỏa mãn: sinC = cosA + cosB. Tìm mệnh đề đúng
A. Tam giác ABC cân tại A
B. Tam giác ABC là tam giác nhọn
C. Tam giác ABC đều
D. Tam giác ABC là tam giác vuông.
- Câu 74 : Cho tứ giác ABCD. Cho hai đường chéo AC và BD vuông góc với nhau. Tìm mệnh đề đúng?
A. AB2 + BC2 = CD2 + AD2
B. AB2 = BC2 + CD2
C. BC2 = AD2 + CD2
D. AB2 + CD2 = BC2 + AD2
- Câu 75 : Cho 4 điểm A, B, C, D thỏa mãn hệ thức AC2 + BD2 = AD2 + BC2. Tìm mệnh đề đúng?
A. AC và AD vuông góc với nhau
B. AC và BD vuông góc với nhau
C. AB và CD vuông góc với nhau
D. AB và BC vuông góc với nhau
- Câu 76 : Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho AM = AC/4, N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?
A. Tam giác BMN là tam giác vuông
B. Tam giác BMN là tam giác cân
C. Tam giác BMN là tam giác đều
D. Tam giác BMN là tam giác vuông cân
- Câu 77 : Cho tam giác đều ABC, độ dài cạnh là 3a . Lấy M, N, P lần lượt nằm trên các cạnh BC, CA, AB sao cho BM = a; CN = 2a và AP = x . Tính x để AM vuông góc với PN.
A. x = a
B. x = 2a
C. x = 0,8.a
D. x = 0,5.a
- Câu 78 : Cho hình chữ nhật ABCD. Kẻ BK ⊥ AC. Gọi M, N lần lượt là trung điểm của AK và CD. Tìm mệnh đề đúng
A. Góc BMN là góc nhọn
B. Góc BMN là góc vuông
C. NB và AC vuông góc với nhau
D. Góc BNM là góc vuông
- Câu 79 : Cho hình thang vuông ABCD có đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = a. Gọi I là trung điểm của CD. Tìm mệnh đề đúng?
A. Góc AIB là góc vuông
B. Tam giác BIC là tam giác vuông
C. AI và BD vuông góc với nhau
D. Tất cả sai
- Câu 80 : Cho tam giác vuông ABC tại C có AC = 9, CB = 5. Tính
A. 25
B. 81
C. 106
D. 53
- Câu 81 : Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2). Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
A. D( 5;0)
B. D( 7; 0)
C. D( 7,5 ;0)
D. tất cả sai
- Câu 82 : Cho hai điểm A(-3; 2), B(4; 3). Biết có 2 điểm M trên trục Ox sao cho tam giác MAB vuông tại M. Tính tổng hoành độ 2 điểm đó.
A. -1
B. 0
C. 1
D. 2
- Câu 83 : Cho hai điểm A(-3; 2), B(4; 3). Tìm tọa độ điểm N trên trục Oy sao cho ΔNAB cân tại N.
A. N(3;0)
B. N( 0; 5)
C. (6; 0)
D. (0;6)
- Câu 84 : Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4). Tìm tọa độ trực tâm H của tam giác ABC?
A. H( 1;1)
B. H( 1; 2)
C. (2;1)
D. (2;2)
- Câu 85 : Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4) . Tìm tọa độ điểm I là tâm đường tròn ngoại tiếp tam giác ABC.
A. I( 1; 2)
B. I(2; 1)
C. I(1; 1)
D. I(2; 2)
- Câu 86 : Cho tam giác vuông ABC tại B, A = 620 và cạnh b = 54. Hỏi a + c gần với giá trị nào nhất?
A. 47,68
B. 25,35
C. 73,03
D. 69,85
- Câu 87 : Cho tam giác ABC đều . Tìm hệ thức sai?
A. b = a cosC + c cosA
B. sinB = sinA cosC + sinC cosA
C. = 2R sinA sinC
D. sinA= cosB.cosC
- Câu 88 : Cho tam giác ABC có a = 7, b = 8, c = 5. Gọi AD là phân giác trong của góc A. Tính AD.
A. 5,2
B. 5,3
C. 5,4
D. 5,5
- Câu 89 : Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
A. 300
B. 600
C. 900
D. 1200
- Câu 90 : Cho ΔABC thỏa mãn c = 2bcosA và
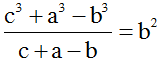 . Tìm mệnh đề đúng?
. Tìm mệnh đề đúng? A. tam giác cân tại C
B. tam giác cân tại B
C. tam giác đều
D. tất cả sai
- Câu 91 : Cho tam giác ABC có cạnh AB = 14, góc C = 1200, tổng hai cạnh còn lại là 16. Tính độ dài hai cạnh còn lại.
C. 5 và 11
A. 8 và 8
D. 10 và 6
B. 7 và 9
C. 5 và 11
D. 10 và 6
- Câu 92 : Tính giá trị biểu thức P = sin300cos150 + sin1500.cos1650
A. P = -0,5
B. P = 0
C. P = 0,5
D. P = 1
- Câu 93 : Cho hai góc bù nhau α và β. Tính giá trị của biểu thức P= cosα.cosβ- sinα.sinβ.
A. P = 0
B. P = 1
C. P = -1
D. P = 2
- Câu 94 : Cho tam giác ABC. Tính P = sinA. cos(B + C) + cos A.sin(B + C).
A. P = 0
A. P = 0
B. P = 1
B. P = 1
C. P = - 1
C. P = - 1
D. P = 2
D. P = 2
- Câu 95 : Cho tam giác ABC. Tính P = cosA.cos( B + C) – sinA.sin(B + C).
A. P = 0
B. P = 1
C. P = -1
D. P = 2
- Câu 96 : Cho biết 3cosα – sinα = 1; 00 < α < 900. Giá trị của tanα bằng:
A. 4/3
B. 3/4
C. 1
D. ½
- Câu 97 : Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai?
- Câu 98 : Cho tam giác ABC có A(1; 2); B(-1; 1) và C(5; -1).Tính cosA.
- Câu 99 : Cho biết cotα = 5. Tính giá trị của E = 2 cos2α + 5sinα.cosα + 1?
- Câu 100 : Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy điểm N sao cho DN = 1 và P là trung điểm BC. Tính cosMNP?
- - Trắc nghiệm Hình học 10 Bài 1 Các định nghĩa
- - Trắc nghiệm Hình học 10 Bài 2 Tổng và hiệu của hai vectơ
- - Trắc nghiệm Hình học 10 Bài 3 Tích của vectơ với một số
- - Trắc nghiệm Hình học 10 Bài 4 Hệ trục tọa độ
- - Trắc nghiệm Ôn tập chương Vectơ - Hình học 10
- - Trắc nghiệm Hình học 10 Bài 1 Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- - Trắc nghiệm Hình học 10 Bài 2 Tích vô hướng của hai vectơ
- - Trắc nghiệm Hình học 10 Bài 3 Các hệ thức lượng trong tam giác và giải tam giác
- - Trắc nghiệm Ôn tập chương Tích vô hướng của hai vectơ và ứng dụng - Hình học 10
- - Trắc nghiệm Toán 10 Bài 1 Mệnh đề

