Lý thuyết con lắc đơn chính xác nhất

Trong chương trình Vật Lý lớp 12 thì bài học về "Con lắc đơn" khá quan trọng với học sinh. Trong bài viết dưới đây Cunghocvui tổng hợp kiến thức lý thuyết như công thức con lắc đơn, lực căng dây con lắc đơn, con lắc đơn có cấu tạo như thế nào, đáp án báo cáo thực hành khảo sát thực nghiệm con lắc đơn,...

I) Con lắc đơn

Ở phần này Cunghocvui gửi đến bạn những kiến thức lý thuyết tổng quát như các công thức con lắc đơn, lực căng dây con lắc đơn, cơ năng của con lắc đơn, năng lượng con lắc đơn, gia tốc của con lắc đơn, chu kì con lắc đơn.

1) Khái niệm

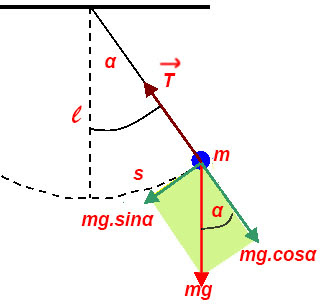
Con lắc đơn là một hệ thống gồm một sợi dây không giãn có khối lượng không đáng kể, chiều dài \(l\), gắn một đầu cố định, đầu còn lại treo vật nặng có khối lượng là \(m\) kích thước không đáng kể coi như chất điểm.

2) Phương trình dao động

• Phương trình theo cung

\(s = S_0cos(wt + \varphi )\)

• Phương trình theo góc

\(\alpha =\alpha _0(wt + \varphi )\)

3) Tần số góc, chu kì con lắc đơn và tần số dao động

• Tần số góc

\(w=\sqrt{\dfrac {g}{l}}\)

• Chu kì dao động

\(T = 2\pi \sqrt{\dfrac {l}{g}}\)

• Tần số dao động

\(f = \dfrac {1}{2\pi}\sqrt{\dfrac {l}{g}}\)

4) Lực căng dây

• Đối với góc \(\alpha >10^0\)

\(T = mg(2cos\alpha - 2cos\alpha_0)\)

• Đối với góc \(\alpha <10^0\)

\(T = mg (1+ \alpha_0^2-\dfrac {3}{2}\alpha^2)\)

5) Gia tốc con lắc đơn

• Gia tốc tiếp tuyến

\(a_{tt}=g.sin\alpha\)

• Gia tốc pháp tuyến

\(a_n=a_{ht}=\dfrac{v^2}{l} = 2g(cos\alpha - cos\alpha_0)\)

• Gia tốc toàn phần

\(a = \sqrt{a_t^2+a_n^2}\)

6) Năng lượng con lắc đơn

Trong phần năng lượng con lắc đơn Cunghocvui gửi đến bạn các công thức tính động năng, thế năng và cơ năng của con lắc đơn ở cả hai trường hợp tổng quát và dao động điều hòa.

6.1) Trường hợp tổng quát (\(\alpha \) bất kì)

• Động năng

\(E_đ = \dfrac {mv^2}{2}\)

• Thế năng

\(E_t = mgh = mgl(2-cos\alpha)\) vì \(h=l(1-cos\alpha)\)

• Cơ năng

\(E = E_đ + E_t = mgl(1-cos\alpha_{max})\)

6.2) Trường hợp dao động điều hòa

• Động năng

\(E_đ = \dfrac {mv^2}{2}=\dfrac {1}{2}mw^2S_0^2sin^2(wt + \varphi )\)

• Thế năng (\(\alpha \leq 10^0\))

\(E_t = \dfrac {1}{2}mgl\alpha^2\)

• Cơ năng

\(E = E_đ + E_t\)

Có thể bạn quan tâm: Tổng hợp công thức con lắc đơn

II) Báo cáo thực hành khảo sát thực nghiệm con lắc đơn

BÁO CÁO THỰC HÀNH: KHẢO SÁT THỰC NGHIỆM CÁC ĐỊNH LUẬT CỦA CON LẮC ĐƠN

 

Nhóm thực hành:................................ Lớp............................

Thành viên:....................................................

A) Mục đích thực hành

.......................................................................................................................................................................................................................................................................................................................................................

B) Cơ sở lý thuyết

2) Cấu tạo con lắc đơn

......................................................................................................................................................................

Cách đo chiều dài con lắc đơn: Dùng............................ (có vạch chia nhỏ nhất đến mm) để do từ.................................đến trọng tâm của...............................

3) Để phát hiện sự phụ thuộc của chi kì T của con lắc đơn với biên độ nhỏ vào biên độ ta cần làm thí nghiệm thay đổi.....................nhưng vẫn giữ nguyên..............dây treo và............quả nặng.

4) Để phát hiện sự phụ thuộc của chu kì T của con lắc đơn với biên độ nhỏ vào khối lượng ta cần làm thí nghiệm thay đổi............dây treo nhưng vẫn giữ nguyên...........dao động và các quả nặng.

5) Để phát hiện sự phụ thuộc của chu kì T của con lắc với biên độ nỏ vào chiều dài l của con lắc đơn ta cần làm thí nghiệm thay đổi.............dây treo nhưng vẫn giữ nguyên............dao động và............các quả nặng.

6) Khi dùng máy đếm thời gian, để dai số của thời gian là 0,01s thì cần chọn thang đo là...........vì thế xác định chu kì T với sai số \(\Delta T = 0,01s\) ta chỉ cần đo thời gian của n = ..... dao động toàn phần.

C) Kết quả

1) Khảo sát ảnh hưởng của biên độ dao động đối với chu kì T của con lắc đơn (Dùng máy đếm thời gian đo chu kì dao động (đo thời gian thực hiện một dao động, với sai số \(\Delta T = 0,01s\) )

Bảng 6.1: m = 50g, l =40cm

A (cm)	\(sin\alpha \approx \alpha = \dfrac{A}{l}\) (rad)	Góc lệch \(\alpha^0 = \dfrac {\alpha.180}{\pi}\)	Chu kì T (s)
\(A_1\) = 3
\(A_2\) = 4
\(A_3\) = 5

- Phát biểu định luật về chu kì của con lắc đơn dao động với biên độ nhỏ:

Chu kì của con lắc đơn dao động với biên độ nhỏ ........ vào biên độ dao động (nhỏ) của con lắc.

2) Khảo sát ảnh hưởng của khối lượng con lắc m đối với chu kì dao động T

Bảng 6.2: \(l = 40cm\), A = 4cm

m(g)	Chu kì T (s)
50
100
200

- Phát biểu định luật về khối lượng của con lắc đơn đối với chu kì dao động T:

Chu kì của con lắc đơn dao động với biên độ nhỏ...........vào khối lượng của con lắc.

3) Khảo sát ảnh hưởng của chiều dài con lắc đơn \(l\) đối với chu kì dao động T

Bảng 6.3: A = 4cm, m = 50g.

Chiều dài \(l\) (m)	Chu kì T (s)	\(T^2\)	\(k=\dfrac {T^2}{l} (s^2/m)\)
\(l_1 = 0,300 \pm ....\)
\(l_2 = 0,400 \pm ....\)
\(l_3 = 0,450 \pm ....\)

Căn cứ vào các kết qua đo và tính được theo bảng 6.3, vẽ đồ thì biểu diễn sự phụ thuộc của T vào l và đồ thị phụ thuộc của \(T^2\) vào \(l\).

• Đồ thị T = f(\(l\))
• Đồ thị \(T^2\) = F(\(l\))

Nhận xét:

a) Đường biểu diễn T = f(\(l\)) có dạng đường...........cho thấy: Chu kì dao động T không.........với độ độ dài l của con lắc đơn.

Đường biểu diễn  \(T^2\) = F(\(l\)) có dạng đường....................đi qua............tọa độ cho thấy: Bình phương chu kì dao động \(T^2\) với độ dài \(l\) của con lắc đơn. \(T^2\)= k.\(l\), trong đó k là hệ số góc của đường biểu diễn \(T^2\) = F(\(l\)).

Từ bảng số liệu 6.3 ta có: \(k=\dfrac{T^2}{l}\)=................ (\(s^2/m\))

Suy ra: \(T = a\sqrt{l}\), với \(a=\sqrt{k}=\)..............(s/\(\sqrt{m}\))

- Phát biểu định luật về chiều dài của con lắc đơn đối với chu kì dao động T:

Chu kì dao động của con lắc đơn dao động với biên độ nhỏ, tại cùng một nơi, không tỉ lệ với.................mà tỉ lệ với...............của dài con lắc.

b) Công thức lí thuyết về chu kì dao động của con lắc đơn dao động với biên độ (góc lệch) nhỏ:

\(T = 2\pi\sqrt{\dfrac{l}{g}}=a\sqrt{l}\) đã nghiệm đúng với tỉ số \(\dfrac {2\pi}{g}=a=...... (s/\sqrt{m})\)'

Từ đó tính được gia tốc trọng trường tại nơi làm thí nghiệm:

\(g = \dfrac {4\pi^2}{a^2} = \dfrac {4\pi^2}{...^2} = ............. (m/s^2)\)

4) Xác định công thức về chu kì dao động của con lắc đơn

Từ các kết quả thực nghiệm suy ra: Chu kì dao động của con lắc đơn dao động với biên độ nhỏ không phụ thuộc vào.....................và...............mà tỉ lệ với.........................của chiều dài \(l\) con lắc đơn và tỉ lệ.....................với........................của gia tốc rơi tự do \(g\) tại nơi làm thí nghiệm.

T =...........................

Trên đây là mẫu đáp án báo cáo thực hành khảo sát thực nghiệm con lắc đơn mà Cunghocvui gửi đến bạn.

III) Luyện tập

Trong phần luyện tập chúng ta đi vào giải quyết các bài tập con lắc đơn căn bản thường gặp để có thể nắm vững kiến thức lý thuyết.

Câu 1: Một con lắc đơn gồm quả cầu có khối lượng bằng 60 g, dây treo dài 90 cm, được treo tại nơi có gia tốc trọng trường  bằng 10 m/s2. Từ vị trí đứng yên cân bằng, truyền cho quả cầu một vận tốc 12 cm/s theo phương ngang cho con lắc dao động điều hòa. Khi dây treo hợp với phương thẳng đứng một góc α=0,02α=0,02 rad thì quả cầu có động năng là:
A. \(3,24.10^{-4} J\)         

B. \(1,62.10^{-4} J\) 

C. \(8,10.10^{-4} J\)

D. \(6,48.10^{-4} J\)

Chọn A

Câu 2: Một con lắc đơn (m = 200 g, ℓ = 80 cm) treo tại nơi có g = 10 m/s2. Kéo con lắc lệch khỏi vị trí cân bằng góc rồi thả không vận tốc ban đầu, con lắc dao động điều hòa với năng lượng E = \(3,2.10^{-4} J\). Biên độ dao động của con lắc bằng:

A. \(S_0\) =3cm

B. \(S_0\) = 2cm

C.  \(S_0\) = 1,8cm

D. \(S_0\) = 1,6cm

Chọn D

Câu 3:  Một con lắc đơn dao động bé với biên độ 4 cm. Thời gian giữa hai lần liên tiếp vận tốc của vật đạt độ lớn cực đại là 0,05 s. Khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ \(S_1\) = 2 cm đến li độ \(S_2\) = 4 cm là:

A. \(\dfrac {1}{120}s\)

B. \(\dfrac {1}{60}s\)

C. \(\dfrac {1}{100}s\)

D. \(\dfrac {1}{80}s\)

Chọn B

Câu 4: Một con lắc đơn được treo trong thang máy, dao động điều hòa với chu kỳ T khi thang máy đứng yên. Nếu thang máy đi lên nhanh dần đều với gia tốc a = 0,1.g thì chu kỳ dao động của con lắc là:

A. \(T\sqrt{\dfrac{9}{10}}\)

B.  \(T\sqrt{\dfrac{10}{11}}\)

C. \(T\sqrt{\dfrac{10}{9}}\)

D. \(T\sqrt{\dfrac{11}{10}}\)

Chọn B

Câu 5:  Con lắc đơn dao động nhỏ, có chiều dài ℓ. Kéo quả cầu lệch khỏi vị trí cân bằng, sao cho quả cầu cách điểm treo một đoạn 0,5ℓ (tính theo phương thẳng đứng) rồi buông nhẹ. Khi qua vị trí thấp nhất, sức căng dây:

A. T = mg

B. phụ thuộc vào ℓ

C. T = 3mg

D. T = 2mg

Chọn D

Trên đây là bài viết Cunghocvui đã tổng hợp về con lắc đơn, hy vọng bài viết sẽ giúp ích cho bạn trong quá trình học tập. Chúc bạn học tập tốt <3