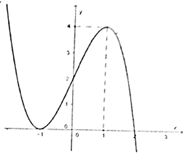
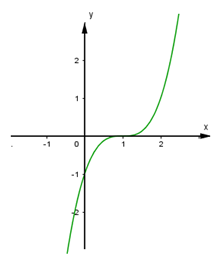
50 bài tập trắc nghiệm khảo sát hàm số mức độ nhận...
- Câu 1 : Đồ thị hàm số: \(y=x^3-mx^2+2m-3\) đi qua điểm A(1;1) khi
A m =3
B m =2
C m =-1
D m =0
- Câu 2 : Cho hàm số y = f(x) xác định trên R\{1} , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ dưới. Mệnh đề nào sau đây đúng?
A Hàm số có cực trị.
B Đồ thị hàm số và đường thẳng y = 3có một điểm chung
C Đồ thị hàm số nhận đường thẳng y = 1 là đường tiệm cận ngang
D Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt.
- Câu 3 : Bảng biến thiên sau đây là của hàm số nào?
A \(y=\frac{x+1}{2x-1}.\)
B \(y=\frac{2x-1}{x+1}.\)
C \(y=\frac{2x+3}{x+1}.\)
D \(y=\frac{2x-1}{x-1}\)
- Câu 4 : Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
A \(y={{\left( x+1 \right)}^{2}}\left( 2-x \right).\)
B \(y=1+2{{x}^{2}}-{{x}^{4}}.\)
C \(y={{x}^{3}}-3x+2.\)
D \(y=x-{{x}^{3}}.\)
- Câu 5 : Cho hàm số \(y=f\left( x \right)\) có đồ thị \(\left( C \right)\) như hình vẽ. Hỏi \(\left( C \right)\) là đồ thị của hàm số nào?
A \(y={{x}^{3}}+1.\)
B \(y={{\left( x-1 \right)}^{3}}.\)
C \(y={{\left( x+1 \right)}^{3}}.\)
D \(y={{x}^{3}}-1.\)
- Câu 6 : Bảng biến thiên dưới đây là của hàm số nào?
A \(y = {x^4} - 2{x^2} - 3\)
B \(y = - {x^4} + 2{x^2} - 3\)
C \(y = {x^4} + 2{x^2} - 3\)
D \(y = {x^4} + 2{x^2} + 3\)
- Câu 7 : Cho hàm số \(y = {x^4} - 2{x^2} + 1.\) Điểm nào sau đây thuộc đồ thị hàm số?
A \(\left( { - 2;\,\,1} \right)\)
B \(\left( {1;\,\,1} \right)\)
C \(\left( {1;\,\,4} \right)\)
D \(\left( {0;\,\,1} \right)\)
- Câu 8 : Cho bảng biến thiên của hàm số y = f(x). Mệnh đề nào sau đây sai?
A Giá trị lớn nhất của hàm số y = f(x) trên tập ℝ bằng 0
B Giá trị nhỏ nhất của hàm số y = f(x) trên tập ℝ bằng –1
C Hàm số y = f(x) nghịch biến trên (–1;0) và (1;+∞)
D Đồ thị hàm số y = f(x) không có đường tiệm cận
- Câu 9 : Đồ thị nào dưới đây là đồ thị của hàm số \(y = {x^3} - 2{{\rm{x}}^2} + 1\)
A
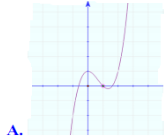
B
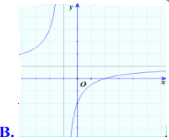
C
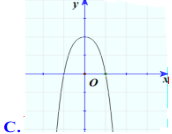
D
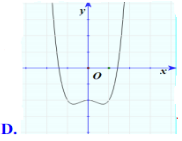
- Câu 10 : Đường cong ở hình dưới đây là đồ thị của một hàm số trong bốn hàm số liệt kê trong bốn phương án A, B, C, D. Hỏi hàm số đó là hàm số nào?
A \(y = {x^4} - 2{x^2} - 1\).
B \(y = - {x^3} + 3x - 1\).
C \(y = {x^3} - {x^2} - 1\).
D \(y = - {x^4} + 2{x^2} - 1\).
- Câu 11 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên khoảng \(\left( {0;2} \right)\) như sau:
A Trên \(\left( {0;2} \right)\), hàm số không có cực trị
B Hàm số đạt cực đại tại \(x = 1\)
C Hàm số đạt cực tiểu tại \(x = 1\)
D Giá trị nhỏ nhất của hàm số là \(f\left( 0 \right)\)
- Câu 12 : Bảng biến thiên trong hình dưới là đồ thị của một số hàm số trong bốn hàm số được liệt kê ở bốn đáp án dưới đây. Hỏi hàm số đó là hàm số nào?
A \(y = \dfrac{{ - x - 3}}{{x - 1}}\)
B \(y = \dfrac{{x + 3}}{{x - 1}}\)
C \(y = \dfrac{{ - x + 3}}{{x - 1}}\)
D \(y = \dfrac{{ - x - 2}}{{x - 1}}\)
- Câu 13 : Hàm số nào trong các hàm số sau đây có đồ thị như hình vẽ:
A \(y = {x^4} - 2{x^2}\)
B \(y = - {x^4} + 2{x^2}\)
C \(y = {x^4} - 2{x^2} + x\)
D \(y = {x^4} - 2{x^2} - 1\)
- Câu 14 : Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ:
A \(y = {x^4} + 2{x^2} - 1\)
B \(y = - {x^4} + 2{x^2} - 1\)
C \(y = {x^4} - 2{x^2} + 1\)
D \(y = {x^4} - 2{x^2} - 1\)
- Câu 15 : Đồ thị của hàm số nào dưới đây có dạng như đường cong ở hình bên dưới?
A \(y = - {x^4} + 6{x^2} - 1\)
B \(y = {x^4} - 6{x^2} - 1\)
C \(y = {x^3} - 6{x^2} + 9x + 1\)
D \(y = {x^3} - 6{x^2} + 9x - 1\)
- Câu 16 : Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A \(y = {x^4} + 2{x^2} + 1\)
B \(y = - {x^4} + 1\)
C \(y = {x^4} + 1\)
D \(y = - {x^4} + 2{x^2} + 1\)
- Câu 17 : Đồ thị của hàm số nào dưới đây có dạng như đường cong hình bên?
A \(y = \dfrac{{x - 1}}{{x + 1}}\)
B \(y = \dfrac{{2x - 1}}{{2x + 1}}\)
C \(y = \dfrac{{x + 1}}{{x - 1}}\)
D \(y = \dfrac{{x - 2}}{{x - 1}}\)
- Câu 18 : Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A \(y = {x^3} + 3{x^2} - 2\)
B \(y = {x^3} - 3{x^2} - 2\)
C \(y = - {x^3} + 3{x^2} - 2\)
D \(y = {x^4} + 3{x^2} - 2\)
- Câu 19 : Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?
A \(y = \dfrac{{x - 1}}{{x + 1}}\)
B \(y = \dfrac{{x + 1}}{{x - 1}}\)
C \(y = \dfrac{{2x - 3}}{{2x - 2}}\)
D \(y = \dfrac{x}{{x - 1}}\)
- Câu 20 : Đồ thị hàm số nào dưới đây có dạng như đường cong ở hình bên dưới?
A \(y = \dfrac{{x + 1}}{{x - 1}}\)
B \(y = \dfrac{{2x - 1}}{{x - 1}}\)
C \(y = \dfrac{x}{{x + 1}}\)
D \(y = \dfrac{{x - 1}}{{x + 1}}\)
- Câu 21 : Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như hình vẽ.
A \(S = 0\)
B \(S = 6\)
C \(S = - 4\)
D \(S = 2\)
- Câu 22 : Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm \(I\left( {1; - 2} \right)\)?
A \(y = \dfrac{{2 - 2x}}{{1 - x}}\).
B \(y = 2{x^3} - 6{x^2} + x + 1\).
C \(y = \dfrac{{2x - 3}}{{2x + 4}}\).
D \(y = - 2{x^3} + 6{x^2} + x - 1\).
- Câu 23 : Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ sau:
A \(a > 0,\,\,b < 0,\,\,c < 0\)
B \(a < 0,\,\,b > 0,\,\,c < 0\)
C \(a > 0,\,\,b > 0,\,\,c < 0\)
D \(a > 0,\,\,b < 0,\,\,c > 0\)
- Câu 24 : Cho đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như sau:
A \(a > 0,\,\,b > 0,\,\,c > 0.\)
B \(a > 0,\,\,b < 0,\,\,c < 0.\)
C \(a > 0,\,\,b < 0,\,\,c > 0.\)
D \(a < 0,\,\,b > 0,\,\,c < 0.\)
- Câu 25 : Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị hàm số như hình bên. Khẳng định nào sau đây là đúng?
A \(a < 0,b < 0,c = 0,d > 0\).
B \(a > 0,b < 0,c > 0,d > 0\).
C \(a < 0,b > 0,c > 0,d > 0\).
D \(a < 0,b > 0,c = 0,d > 0\).
- Câu 26 : Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
A \(\left[ \begin{array}{l}b > \dfrac{2}{3}\\b < 0\end{array} \right.\).
B \(0 < b < \dfrac{1}{6}\).
C \(0 < b < \dfrac{2}{3}\).
D \(\left[ \begin{array}{l}b > \dfrac{1}{6}\\b < 0\end{array} \right.\).
- Câu 27 : Biết rằng hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị là đường cong như hình vẽ bên dưới.
A \(f\left( {3a + 2b + c} \right) = - 1\)
B \(f\left( {3a + 2b + c} \right) = - 144\)
C \(f\left( {3a + 2b + c} \right) = - 113\)
D \(f\left( {3a + 2b + c} \right) = 1\)
- Câu 28 : Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây là đúng?
A \(a > 0,\,\,b > 0,\,\,c < 0,\,\,d > 0\)
B \(a < 0,\,\,b < 0,\,\,c < 0,\,\,d > 0\)
C \(a > 0,\,\,b < 0,\,\,c < 0,\,\,d > 0\)
D \(a > 0,\,\,b < 0,\,\,c > 0,\,\,d > 0\)
- Câu 29 : Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây ?
A \(y = {x^3} - 3{x^2} + 2\)
B \(y = - {x^3} + 3{x^2} - 2\)
C \(y = {x^4} + {x^2} + 2\)
D \(y = - {x^4} - {x^2} + 2\)
- Câu 30 : Cho hàm số \(y = a{x^3} + b{x^2} + cx + d,\,\,\,a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\) có đồ thị như hình vẽ. Tính \(S = a + b.\)
A \(S = 0\)
B \(S = 1\)
C \(S = - 2\)
D \(S = - 1\)
- Câu 31 : Đường cong trong hình vẽ bên là của hàm số nào trong 4 hàm số dưới đây?
A \(y = - {x^4} + 2{x^2} - 1\)
B \(y = - {x^3} + 3{x^2} - 1\)
C \(y = {x^4} - {x^2} - 4\)
D \(y = {x^4} - 2{x^2} - 1\)
- Câu 32 : Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\)\(\left( {d < 0} \right)\) có đồ thị như hình bên. Khẳng định nào dưới đây là đúng?
A \(a < 0,\,\,b > 0,\,\,c < 0\)
B \(a > 0,\,\,b > 0,\,\,c > 0\)
C \(a > 0,\,\,b > 0,\,\,c < 0\)
D \(a > 0,\,\,b < 0,\,\,c > 0\)
- Câu 33 : Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
A \(y = \dfrac{{x - 2}}{{x + 1}}\)
B \(y = \dfrac{{x + 2}}{{x + 1}}\)
C \(y = \dfrac{{x - 2}}{{x - 1}}\)
D \(y = \dfrac{{x + 2}}{{x - 2}}\)
- Câu 34 : Hàm số nào sau đây có đồ thị như hình bên ?
A \(y = - {x^4} - 2{x^2} + 1.\)
B \(y = {x^4} - 3{x^2} + 1.\)
C \(y = - {x^4} + 2{x^2} + 1.\)
D \(y = {x^4} - 2{x^2} + 1.\)
- Câu 35 : Hàm số nào dưới đây có bảng biến thiên như hình vẽ
A \(y = \dfrac{{x + 2}}{{x + 1}}\).
B \(y = \dfrac{{x - 3}}{{x - 1}}\).
C \(y = \dfrac{{ - x + 2}}{{x - 1}}\).
D \(y = \dfrac{{x + 2}}{{x - 1}}\).
- Câu 36 : Đồ thị sau là đồ thị của hàm số nào trong bốn phương án A, B, C, D
A \(y = {x^3} - 3{x^2} + 2\).
B \(y = {x^3} - 3x + 1\).
C \(y = {x^3} - 3{x^2} + 1\).
D \(y = - {x^3} - 3{x^2} + 1\).
- Câu 37 : Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
A \(a > 0;\,\,b > 0;\,\,c > 0;\,\,d < 0.\)
B \(a < 0;\,\,b > 0;\,\,c < 0;\,\,d < 0.\)
C \(a < 0;\,\,b > 0;\,\,c > 0;\,\,d < 0.\)
D \(a < 0;\,\,b < 0;\,\,c > 0;\,\,d < 0.\)
- Câu 38 : Cho hàm số\(y = \dfrac{{ax + 1}}{{bx + c}}\) (với a, b, c là các tham số) có bảng biến thiên như sau:
A \(4\).
B \(3\).
C \(2\).
D \(1\).
- Câu 39 : Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình bên. Trong các hệ số a, b, c và d có bao nhiêu số âm?
A \(1\)
B \(3\)
C \(2\)
D \(4\)
- Câu 40 : Cho hàm số \(y = \left( {x + 2} \right){\left( {x - 1} \right)^2}\) có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với hàm số \(y = \left| {x + 2} \right|{\left( {x - 1} \right)^2}\)?
A Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
B Hàm số nghịch biến trên khoảng \(\left( { - 1;2} \right)\).
C Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
D Hàm số đồng biến trên khoảng \(\left( { - 2;0} \right)\).
- Câu 41 : Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) với \(a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\), \(c \ne 0\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng \(3\). Giá trị của \(f\left( { - 2} \right)\) bằng:
A \( - 3\)
B \( - 5\)
C \( - 2\)
D \( - 1\)
- Câu 42 : Cho hàm số \(y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).\) Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
A 8 đvdt
B 6 đvdt
C 4 đvdt
D 10 đvdt
- Câu 43 : Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
A \(b + c + d = 1\)
B \(b + c + d = 3\)
C \(b + c + d = 5\)
D \(b + c + d = 10\)
- Câu 44 : Cho đường cong \(\left( C \right):y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
A \(a > 0,b < 0,c < 0,d < 0\).
B \(a > 0,b > 0,c < 0,d > 0\).
C \(a < 0,b > 0,c > 0,d < 0\).
D \(a > 0,b > 0,c < 0,d < 0\).
- Câu 45 : Hãy xác định a, b, c để hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ
A \(a = \frac{1}{4},\,\,b = - 2,\,\,c = 2\)
B \(a = 4,\,\,b = - 2,\,\,c = 2\)
C \(a = 4,\,\,b = 2,\,\,c = 2\)
D \(a = \frac{1}{4},\,\,b = - 2,\,\,c > 0\)
- Câu 46 : Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A \(y = \left| {{x^3}} \right| - 3\left| x \right|\).
B \(y = \left| {{x^3} + 3x} \right|\).
C \(y = \left| {{x^3}} \right| + 3\left| x \right|\).
D \(y = \left| {{x^3} - 3x} \right|\).
- Câu 47 : Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ bên. Tìm kết luận đúng.
A \(a + b > 0\)
B \(bc > 0\)
C \(ab > 0\)
D \(ac > 0\)
- - Trắc nghiệm Toán 12 Chương 2 Bài 1 Lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 2 Hàm số lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 4 Hàm số mũ và hàm số lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 5 Phương trình mũ và phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 6 Bất phương trình mũ và bất phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 3 Bài 1 Nguyên hàm
- - Trắc nghiệm Toán 12 Chương 3 Bài 2 Tích phân
- - Trắc nghiệm Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học
- - Trắc nghiệm Toán 12 Bài 1 Số phức
- - Trắc nghiệm Toán 12 Bài 2 Cộng, trừ và nhân số phức