Vật lí 9 Định luật bảo toàn năng lượng

Vật lý 9 Định luật bảo toàn năng lượng

Cùng Cunghocvui tìm hiểu về những nội dung lý thuyết quan trọng và giải bài tập về lý thuyết và trả lời cho câu hỏi định luật bảo toàn năng lượng của ai!

I. Lý thuyết

1. Động lượng

    a) Xung lực F

   Tác động một lực F có phương và hương xác định trong quá trình truyền lực không có sự thay đổi về tác động của lực. Ta nhận thấy cần mất một khoảng thời gian t để quá trình truyền lực hoàn tất. Khi đó ta định nghĩa xung của lực sẽ là mối quan hệ tương tác giữa F và t. 

    b) Động lượng

    * Công thức:

\(m\vec a= \vec F \Leftrightarrow \dfrac{\vec v_2-\vec v_1}{\Delta t}=\vec F\)

\(m\vec v_2-m\vec v_1=\vec F. \Delta t\)

    * Tương quan giữa xung lực và động lượng:

    Ta có: \(\vec p_2 - \vec p_1 = \vec F.Δt \ hay \ \vec Δp = \vec F.Δt\)

Ý nghĩa: Công thức thể hiện mối tương quan giữa động lực tác động lên xung lực khiến nguồn năng lượng được giải phóng

2. Định luật bảo toàn động lượng

    - Xét trong môi trường hệ kín, khái niệm của định luật bảo toàn năng lượng:

        + Ta nhận thấy các vật tương tác với nhau theo mối quan hệ cân bằng giữa chúng đều có những sự tương tác với nhau khiến cho vật chuyển động.

        + Có hai mối quan hệ tương quan với nhau đó chính là nội lực và ngoại lực. Hai hệ này luôn có sự tương tác lẫn nhau và đây là nguyên nhân tạo ra sự cân bằng lực.

    - Công thức biểu diễn ý nghĩa

    \(\vec p_1+ \vec p_2 + ... + \vec p_n = const\)

2. Công và công suất

a. Công

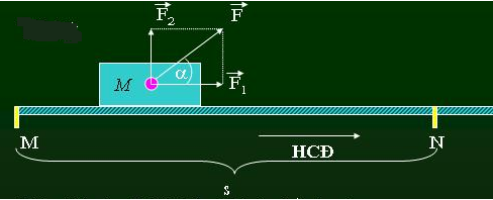
    - Công được tạo ra khi ta tác động một lực F như đã phân tích trên vào một vật chủ gây ra nội lực đẩy vật chuyển động:

    - Công thức tính: \(A = F.s.cosα\)

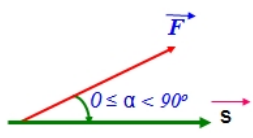
    - Điều kiện: Khi \(0 ≤ α < 90^0 \ thì \ cosα > 0 ⇒ A > 0\)

    ⇒ Giá trị của công có thể điều chỉnh và luôn thay đổi theo thời gian

        + Khi \(α = 90^0 \ thì \ A = 0\)

    ⇒ Khi đó phương và hướng của lực được xác định là nằm vuông góc với phương xét vật.

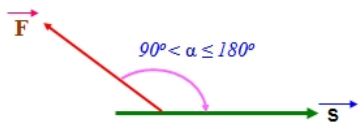
        + Khi \(90^0 < α ≤ 180^0 \ thì \ cosα < 0 ⇒ A < 0\)

    ⇒ Lực trong trường hợp này ngược chiều so với các dạng trường hợp khác ở chỗ tạo ra lực âm

b. Công suất

    Ta ký hiệu là P được xác định bởi công thức chuyển đổi sau đây:

\(P =\dfrac{A}{t}\)

   Giải thích các đại lượng:

•         A là công (J)
•         t khoảng thời lượng cần thiết để hoàn thành công A (s)
•         P là công năng suất tích lũy của vật chuyển động (W)

    \(1 W = 1 J/s\)

    Chú ý:

    - Một số chú ý về ứng dụng của năng lượng công vào trong thực tiễn đời sống:

        + Ngoài đơn vị là  J thì A còn được đo bằng một dạng đơn vị phổ biến là HP

  \(  1 HP = 736 W\)

        + Thực tế về đơn vị (W.h)

  \( 1 W.h = 3600 J\)

  \(  1 kW.h = 3600000 J\)

3. Các dạng năng lượng

- Động năng

\(W_đ=\dfrac{1}{2}mv^2\)

\(A=\dfrac{1}{2}mv_2^2-\dfrac{1}{2} mv_1^2\)

- Thế năng trọng trường

\(W_t = mgz\)

- Thế năng đàn hồi

\(A=\dfrac{1}{2}k(\Delta l)^2\)

\(W_t=\dfrac{1}{2}k(\Delta l)^2\)

- Cơ năng:

+ Trong trường:

\(W=W_đ+Wt=\dfrac{1}{2}mv^2+\dfrac{1}{2}mgz\)

 \(\dfrac{1}{2}mv^2+\dfrac{1}{2}mgz = const\)

+ Đàn hồi:

\(W=\dfrac{1}{2}mv^2+\dfrac{1}{2}k(\Delta l)^2\)

Nếu được bảo toàn ta rút ra được kết luận:

\(W=\dfrac{1}{2}mv^2+\dfrac{1}{2}k(\Delta l)^2=const\)

II. Bài tập vận dụng

Bài 1: Hiện tượng các dạng năng lượng được chuyển hóa qua lại lẫn nhau trong thực tế xảy ra như thế nào. Nêu tính ứng dụng của định luật bảo toàn năng lượng trong trường hợp kể trên? Cho ví dụ:

Đáp án

Có rất nhiều hiện tượng trong đời sống minh chứng cho sự chuyển hóa này, và việc chuyển hóa luôn được đảm bảo quá trình bảo toàn lẫn nhau. Đặc biệt có thể thấy đó là hiện tượng đàn hồi của vật. Khi chúng ta kích hoạt vật có tính đàn hồi, thế năng sẽ chuyển hóa thành động năng, công của chúng là không thay đổi trong suốt quá trình.

Bài 2: Sử dụng bình cách nhiệt để chứa đựng một nguồn nước có thể tích 2 lít. Sau khi cho tác dụng thì quá trình này xảy ra hiện tượng đốt cháy, nhiệt độ tăng dần từ 20 độ lên 80 độ C. Nhiệt năng được chuyển hóa từ năng lượng của dòng điện, tính nhiệt lượng tỏa ra.

Đáp án

Áp dụng công thức: \(Q = cm(t_2 – t_1)\)

Ta có:

\(Q = cm(t_2 – t_1) = 4 200.2.(80 – 20) = 504000J.\)

Định luật bảo toàn năng lượng

Với những gì Cunghocvui đã giúp các bạn giải quyết về khái niệm về định luật bảo toàn năng lượng trên đây, hy vọng rằng sẽ giúp các bạn đạt được kết quả cao trong học tập!