Giải bài 88 trang 111 - Sách giáo khoa Toán 8 tập 1
Đề bài
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:
a) Hình chữ nhật?
b) Hình thoi?
c) Hình vuông?
Hướng dẫn giải
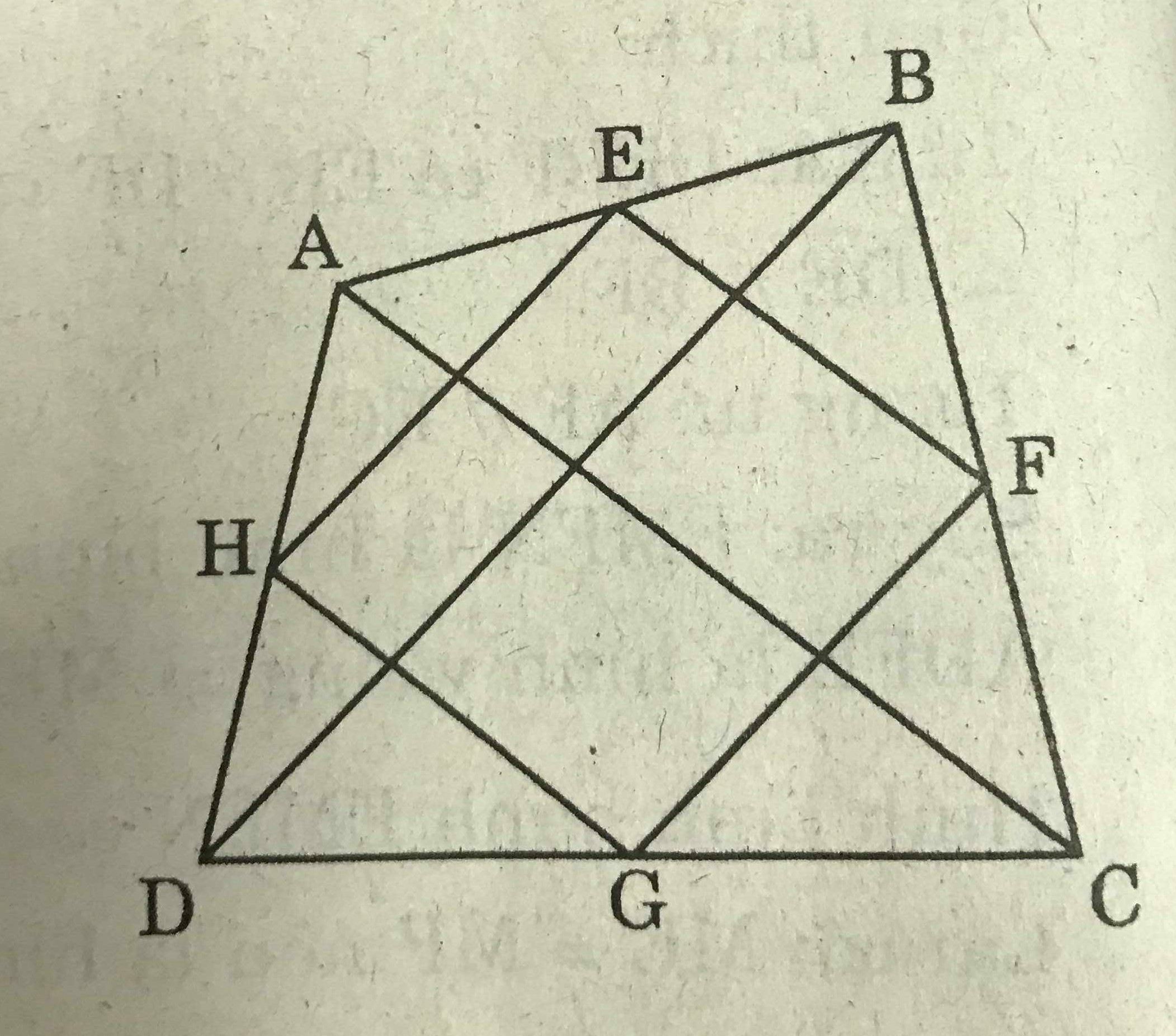
EF là đường trung bình của \(\triangle\)ABC => EF // AC và EF = \(\dfrac{AC}{2}\)
GH là đường trung bình của \(\triangle\)ADC => GH // AC và GH = \(\dfrac{AC}{2}\)
Nên tứ giác EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật
\(\Leftrightarrow\) EH \(\perp\) EF
Lại có : EH // BD (EH là đường trung bình của \(\triangle\)ABD)
EF // AC
Do đó : AC \(\perp\) BD.
Điều kiện phải tìm : Các đường chéo AC và BD vuông góc với nhau.
b) Hình bình hành EFGH là hình thoi
\(\Leftrightarrow\) EH = EF
Lại có : EH = \(\dfrac{BD}{2}\) (EH là đường trung bình của \(\triangle\)ABD)
EF = \(\dfrac{AC}{2}\)
Do đó : AC = BD
Điều kiện phải tìm : Các đường chéo AC và BD bằng nhau.
c) Hình bình hành EFGH là hình vuông
\(\Leftrightarrow\) EF = EF và EH \(\perp\) EF
\(\Leftrightarrow\) AC = BD và AC \(\perp\) BD
Điều kiện phải tìm : Các đường chéo AC và BD bằng nhau và vuông góc với nhau.

