Lý thuyết điện trường và cường độ điện trường đường sức điện

Lý thuyết điện trường và cường độ điện trường đường sức điện

Bài viết dưới đây Cunghocvui sẽ giúp các bạn làm sáng tỏ nội dung lý thuyết và bài giải điện trường và cường độ điện trường đường sức điện!

I. Điện trường

1. Định nghĩa:

- Điện trường là một môi trường đặc biệt trong điện từ học bao quanh các điện tích. Đặc trưng của môi trường này là tác dụng lực (được gọi là lực điện) lên một điện tích nằm trong môi trường đó.

- Đơn vị của điện trường: V/m (Volt trên mét) hoặc N/C (Newton trên Coulomb).

- Điện trường rất quan trọng trong nhiều lĩnh vực vật lý và được khai thác thực tế trong công nghệ điện. Ở quy mô nguyên tử, điện trường là lực tương tác chính giữa hạt nhân và các electron trong nguyên tử. Điện trường và từ trường đều là biểu hiện của lực điện từ, một trong bốn lực cơ bản (hoặc tương tác) của tự nhiên.

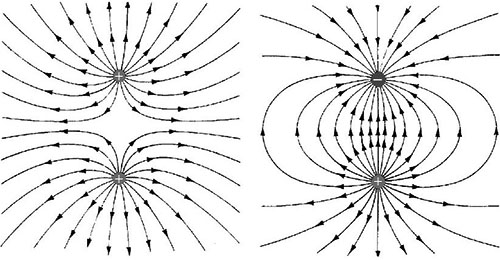
- Điện trường là đại lượng vật lý có hướng (vector), được biểu diễn thông qua vector cường độ điện trường (thường được ký hiệu là E). Cường độ điện trường trong không gian có thể được biểu diễn bằng các đường sức điện trường. Vector cường độ điện trường có phương trùng với phương tiếp tuyến của đường sức điện trường và có chiều trùng với chiều của đường sức điện trường. Tập hợp các đường sức cường độ điện trường gọi là điện phổ.

2. Cường độ điện trường

- Cường độ điện trường là đại lượng đặc trưng cho điện trường về phương diện tác dụng lực.

- Một điện tích, q, nằm trong điện trường có cường độ điện trường, thể hiện bằng vectơ \({\displaystyle {\vec {E}}}\), chịu lực tĩnh điện, thể hiện bằng vector lực \({\displaystyle {\vec {F}}}\), tính theo biểu thức:

\({\displaystyle {\vec {F}}=q.{\vec {E}}}\)

Vậy, \({\displaystyle {\vec {E}}={\vec {F}}/q}\)

- Cường độ điện trường gây ra bởi điện tích điểm được tính bằng công thức:

\({\displaystyle E={\frac {q}{4\pi \ \varepsilon _{0}\varepsilon \ r^{2}}}}\)

trong đó

• q là độ lớn điện tích
• \({\displaystyle \varepsilon _{0}}\) là độ điện thẩm chân không
• \({\displaystyle \varepsilon \ }\) là hằng số điện môi của môi trường
• r là khoảng cách từ điện tích đến điểm ta xét

- Với cường độ điện trường này, một điện tích khác nằm trong nó sẽ chịu lực điện tỷ lệ với tích hai điện tích và tỷ lệ nghịch với bình phương khoảng cách. Đó chính là lực Coulomb.

- Để tính được điện trường do một vật mang điện gây ra, có thể chia nó ra thành nhiều vật nhỏ hơn. Nếu phép chia tiến đến một giới hạn nào đó, vật nhỏ mang điện sẽ trở thành một điện tích. Khi đó có thể áp dụng nguyên lý chồng chất cho điện trường (hay còn gọi là nguyên lý tác dụng độc lập).

- Cường độ điện trường tại một điểm trong điện trường do N điện tích điểm gây ra bằng tổng vectơ cường độ điện trường do từng điện tích điểm gây ra tại điểm đó.

3. Điện thế

- Như mọi trường véctơ có dạng tỷ lệ nghịch với bình phương khoảng cách (ví dụ như lực hấp dẫn), trường véc tơ cường độ điện trường là một trường véctơ bảo toàn. Điều này nghĩa là mọi tích phân đường của véctơ cường độ điện trường E từ vị trí r0 đến r:

\({\displaystyle \int _{\mathbf {r} _{0}}^{\mathbf {r} }\mathbf {E} \cdot d\mathbf {r} '}\) đều có giá trị không phụ thuộc vào đường đi cụ thể từ r0 đến r.

- Như vậy tại mỗi điểm r đều có thể đặt giá trị gọi là điện thế:

\({\displaystyle \phi (\mathbf {r} )-\phi (\mathbf {r} _{0})=\int _{\mathbf {r} _{0}}^{\mathbf {r} }\mathbf {E} \cdot d\mathbf {r} '}\)

\({\displaystyle \phi (\mathbf {r} )=\phi (\mathbf {r} _{0})+\int _{\mathbf {r} _{0}}^{\mathbf {r} }\mathbf {E} \cdot d\mathbf {r} '}\)

với φ(r0) là giá trị điện thế quy ước ở mốc r0.

II. Cường độ điện trường

1. Định nghĩa

- Cường độ điện trường tại một điểm là một đại lượng vật lý, thể hiện bằng vectơ trong không gian, đặc trưng cho độ lớn và hướng của điện trường về mặt tác dụng lực tại điểm đó.

- Giả sử ta đặt một điện tích \({\displaystyle q_{0}\,}\) tại một điểm M nào đó trong điện trường, điện tích này phải có giá trị đủ nhỏ để nó không làm thay đổi điện trường mà ta đang xét (gọi là điện tích thử). Như vậy, điện tích \({\displaystyle q_{0}\,}\) sẽ bị điện trường tác dụng một lực \({\displaystyle {\vec {F}}}.\) - Thực nghiệm chứng tỏ tỉ số \({\displaystyle {{\vec {F}} \over q_{0}}}\) không phụ thuộc vào điện tích \({\displaystyle q_{0}\,}\) mà chỉ phụ thuộc vị trí của điểm M, nghĩa là, tại mỗi điểm xác định trong điện trường, tỉ số:

\({\displaystyle {\vec {E}}={{\vec {F}} \over q_{0}}={\vec {const}}\,}\) (*)

- Theo đó, \( {\displaystyle {\vec {E}}}\) được gọi là vectơ cường độ điện trường, theo nghĩa ta có thể dùng \({\displaystyle {\vec {E}}}\) để đặc trưng cho điện trường (về mặt tác dụng lực) tại điểm đang xét. Độ lớn E gọi là cường độ điện trường.

- Từ biểu thức (*) ta thấy nếu chọn\( {\displaystyle q_{0}=+1\,}\) thì \({\displaystyle {\vec {E}}={\vec {F}}} \) nghĩa là:

- "Véctơ cường độ điện trường tại một điểm là một đại lượng có trị vectơ bằng lực tác dụng của điện trường lên một đơn vị điện tích dương đặt tại điểm đó."

- Trong hệ đơn vị SI, cường độ điện trường được tính bằng \({\displaystyle {V \over m}}.\)

2. Vectơ cường độ điện trường gây bởi một điện tích điểm

- Vectơ cường độ điện trường gây bởi một điện tích điểm.

- Dựa vào định nghĩa trên, ta xác định được vectơ cường độ điện trường \({\displaystyle {\vec {E}}}\) gây bởi điện tích điểm q tại điểm M:

\({\displaystyle {\vec {E}}={{\vec {F}} \over q_{0}}={1 \over {4\pi \ \sigma _{0}}}.{q \over {\sigma r^{2}}}.{{\vec {r}} \over r}\,}\) (**)

- Từ (**) ta nhận thấy:

• Nếu q là điện tích dương, thì vectơ cường độ điện trường \({\displaystyle {\vec {E}}}\) do nó gây ra sẽ cùng hướng với bán kính\( {\displaystyle {\vec {r}}}\) (hình a) nghĩa là \({\displaystyle {\vec {E}}}\) hướng ra xa điện tích q.
• Nếu q là điện tích âm, thì vectơ cường độ điện trường \({\displaystyle {\vec {E}}}\) do nó gây ra sẽ ngược hướng với bán kính \( {\displaystyle {\vec {r}}}\) (hình b) nghĩa là \({\displaystyle {\vec {E}}}\) hướng vào điện tích q.
• Trong cả hai trường hợp trên, cường độ điện trường tại  M đều có dạng:

\({\displaystyle E={1 \over {4\pi \ \sigma _{0}}}.{|q| \over {\sigma r^{2}}}\,}\)

3. Vectơ cường độ điện trường gây bởi 1 hệ vật mang điện

- Xét một hệ điện tích điểm \({\displaystyle q_{1}\,},{\displaystyle q_{2}\,},...,{\displaystyle q_{n}\,}\) được phân bố không liên tục trong không gian. Để xác định vectơ cường độ điện trường tổng hợp \({\displaystyle {\vec {E}}}\) tại một điểm M nào đó trong điện trường của hệ điện tích điểm đó, ta tưởng tượng đặt tại M một điện tích \({\displaystyle q_{0}\,}\). Theo đó, lực tổng hợp tác dụng lên \({\displaystyle q_{0}\,}\) bằng:

\({\displaystyle {\vec {F}}=\sum _{i=1}^{n}{\vec {F_{i}}}\,}\)

- Trong đó \({\displaystyle {\vec {F_{i}}}}\) là lực tác dụng của \({\displaystyle q_{i}\,}\) lên \({\displaystyle q_{0}\,}.\)

- Như vậy, vectơ cường độ điện trường tổng hợp tại M bằng:

\({\displaystyle {\vec {E}}={{\vec {F}} \over q_{0}}={{\sum _{i=1}^{n}{\vec {F_{i}}}} \over q_{0}}=\sum _{i=1}^{n}{{\vec {F_{i}}} \over q_{0}}\,}\)

- Nhưng \({\displaystyle {{\vec {F_{i}}} \over q_{0}}={\vec {E_{i}}}\,}\) chính là vectơ cường độ điện trường do điện tích \({\displaystyle q_{i}\,}\) gây ra tại M nên:

\({\displaystyle {\vec {E}}=\sum _{i=1}^{n}{\vec {E_{i}}}\,}\)

- Từ công thức trên, ta có thể phát biểu:

- Vectơ cường độ điện trường gây bởi một hệ điện tích điểm bằng tổng các vectơ cường độ điện trường gây ra bởi từng điện tích điểm của hệ.

- Đó chính là phát biểu của Nguyên lý chồng chất điện trường.

Bài tập về điện trường và cường độ điện trường đường sức điện

III. Đường sức điện

1. Định nghĩa

Đường sức của điện trường là đường mà tiếp tuyến với nó tại mỗi điểm trùng với phương của vectơ cường độ điện trường tại điểm đó,chiều của đường sức là chiều của vectơ cường độ điện trường (H.15.2) tại điểm đó.

2. Tính chất

- Vì điện trường có ở tất cả mọi điểm trong không gian bao quanh điện tích, nên qua bất kì điểm nào cũng có thể vẽ được một đường sức.

- Vì tại mỗi điểm cường độ điện trường có hướng và độ lớn xác định, nênqua mỗi điểm chỉ có thể vẽ được một đường sức, hay nói khác đi, các đường sức không cắt nhau.

- Để cho các đường sức có thể biểu diễn cả độ lớn của cường độ điện trường người ta quy ước vẽ đường sức mau ở nơi cường độ điện trường lớn, đường sức thưa ở nơi cường độ điện trường nhỏ.

- Dạng điện trường đơn giản nhất, thường gặp trong thực tế là điện trường đều. Đó là điện trường mà cường độ của nó có cùng một độ lớn và hướng ở mọi điểm. Đường sức của điện trường đều là những đường thẳng song song cách đều nhau. Một ví dụ thường gặp của điện trường đều là điện trường ở khoảng giữa hai bản phẳng kim loại tích điện bằng nhau và trái dấu, đặt song song với nhau, còn ở gần bờ các bản kim loại, điện trường không đều.

III. Bài tập áp dụng

Bài 1: Tìm độ dài AC và BC dưới hình vẽ.

Lời giải:

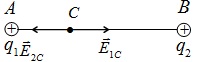
Gọi điểm cần tìm là C mà tại đó cường độ điện trường tổng hợp do \(q_1, q_2\) gây ra bằng không. Theo đề bài ta có:

\(\vec E=\vec {E_{1C}}+\vec {E_{2C}}=\vec 0\rightarrow \vec {E_{1C}}=\vec {E_{2C}} (1)\)

( Hai vectơ \(\vec {E_{1C}},\vec {E_{2C}}\) là hai vectơ đối ).

Từ (1) →q1.q2 >0  cùng phương \(\vec {E_{2C}}\)→ C thuộc đường thẳng AB.

Từ (1) →\(\vec {E_{1C}}\)  ngược chiều\(\vec {E_{2C}}\)  và \(q_1, q_2\) cùng dấu (\(q_1.q_2 >0\))

 → C nằm trong đoạn thẳng AB →  AC + CB = AB  (2)                       

Từ (1) \(\vec {E_{1C}}\)=\(\vec {E_{2C}}\) \(→E_{1C}=E_{2C}  \)

\(k.\dfrac{d_1}{eAC}=k\dfrac{q_2}{eBC}\rightarrow \dfrac{|q_1|}{|q_2|}=\dfrac{AC^2}{BC^2}\rightarrow \dfrac{AC}{BC}=\sqrt{\dfrac{|q_1|}{|q_2|}}=\sqrt{\dfrac{5.10^{-8}}{20.10^{-8}}}=\dfrac{1}{2}\)

Hay BC = 2AC  (3).

Từ (2) và (3) giải ra ta có kết quả: AC = 10cm, BC = 20cm.

Bài 2: Điện tích q được đặt trong mọt môi trường có hệ số điện dung riêng là 81. Điện tác động gây ra một điện trường \(E =1.5.10^4 V/m\) vào một điểm M cách nó khoảng 26cm. Tính lực tác dụng vào vật N cách điện tích một đoạn 17cm.

Lời giải:

Do \(E=\dfrac{1}{r^2}\) nên \(\dfrac{E_M}{E_N}=(\dfrac{r_N}{r_M})^2\rightarrow \dfrac{1.5}{E_M}=(\dfrac{17}{26})^2 \rightarrow E_M=3.5.10^4\)

Với những gì mà Cunghocvui đã giúp các bạn khái quát nội dung và bài tập điện trường và cường độ điện trường đường sức điện trên đây, hy vọng sẽ giúp các bạn đạt kết quả cao trong học tập!