Hình viên phân - Công thức tính diện tích chính xác nhất

Hình viên phân - Công thức tính diện tích chính xác nhất

Chắc hẳn các bạn học sinh đã được làm quen với khái niệm hình viên phân nhưng ở mức độ kiến còn cơ bản. Tuy nhiên, liệu bạn đã nắm chắc công thức tính diện tích cũng như những ứng dụng của nó hay chưa. Vậy các bạn học sinh có đang gặp vấn đề về cách tính diện tích hình viên phân thì bài viết sẽ là sự lựa chọn hợp lý trong việc tìm kiếm những lời giải!

I. Định nghĩa 

Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy.

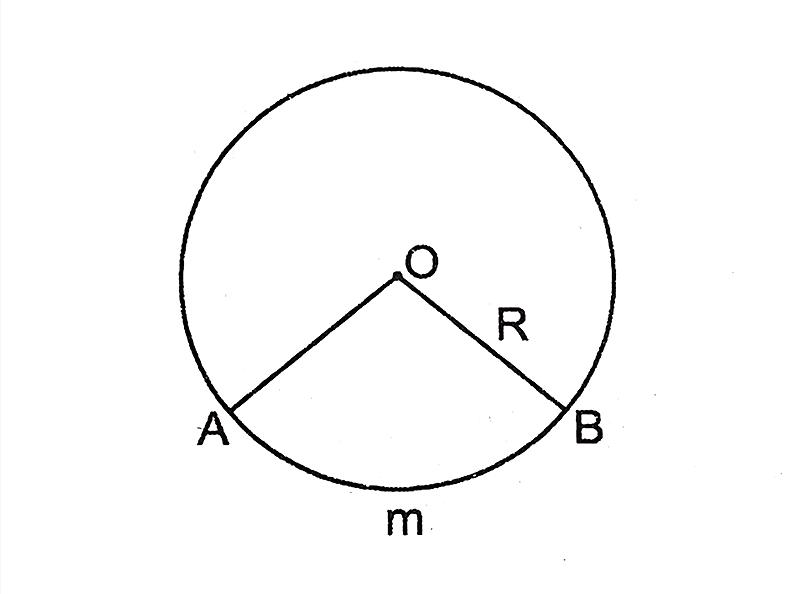
Trong đó:

• Dây cung AB có độ dài là m
• R là bán kình hình tròn giới hạn

II. Công thức tính diện tích hình viên phân

1. Cách tính diện tích hình viên phân được thể hiện qua công thức sau đây

\({\displaystyle {\dfrac {1}{2}}r^{2}(\theta -\sin {\theta })}\)

Để tính diện tích hình viên phân, cần lấy diện tích hình quạt tròn giới hạn bởi dây cung và hai bán kính trừ đi diện tích hình tam giác tạo bởi tâm đường tròn và hai điểm mút của dây cung.

Xem thêm: Công thức tính diện tích hình viên phân

2. Công thức tính diện tích hình tròn giới hạn:

• Diện tích phần giới hạn bởi cung tròn và tâm đường tròn là:

\({\displaystyle A={\dfrac {1}{2}}r^{2}\theta .}\)

• Chia hai vế cho \({\displaystyle {\pi r^{2}}}\)
• Tỷ lệ giữa diện tích A và diện tích phần giới hạn trong đường tròn bằng với tỷ lệ giữa số đo góc \({\displaystyle \theta }\) và số đo góc cả đường tròn:

\({\displaystyle {\dfrac {A}{\pi r^{2}}}={\dfrac {\theta }{2\pi }}.}\)

• Giản lược \({\displaystyle \pi }\) ở cả hai vế

\({\displaystyle {\dfrac {A}{r^{2}}}={\dfrac {\theta }{2}}.}\)

• Nhân hai vế với \({\displaystyle r^{2}}\), thu được

\({\displaystyle A={\dfrac {1}{2}}r^{2}\theta .}\)

• Tương tự phần trên, công thức tương đương nếu số đo góc đo bằng độ:

\({\displaystyle A={\dfrac {\alpha }{360}}\pi r^{2}.}\)

III. Bài tập 

Câu 1: Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm AOB = 60 độ và bán kính đường tròn là 5.1cm?

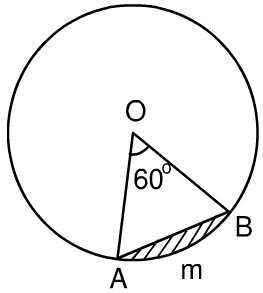
Lời giải:

Ta có S viên phân = S quạt AOB - S tam giác AOB

S quạt AOB = \(\dfrac{\pi. R^2.n}{360 ^{\circ}}= \dfrac{\pi. 5,1^2.60^{\circ}}{360 ^{\circ}}= 13,61(cm^2)\)

S tam giác AOB = \(\dfrac{R^2\sqrt3}{4}= \dfrac{5,1^2\sqrt3}{4}= 11,26 (cm^2)\)

\(Svp= 13,61-11,26= 2,35(cm^2)\)
Câu 2: Cho hình viên phân có dây BC = a cung \(BC=90^0\). Tính diện tích hình viên phân.

Lời giải:

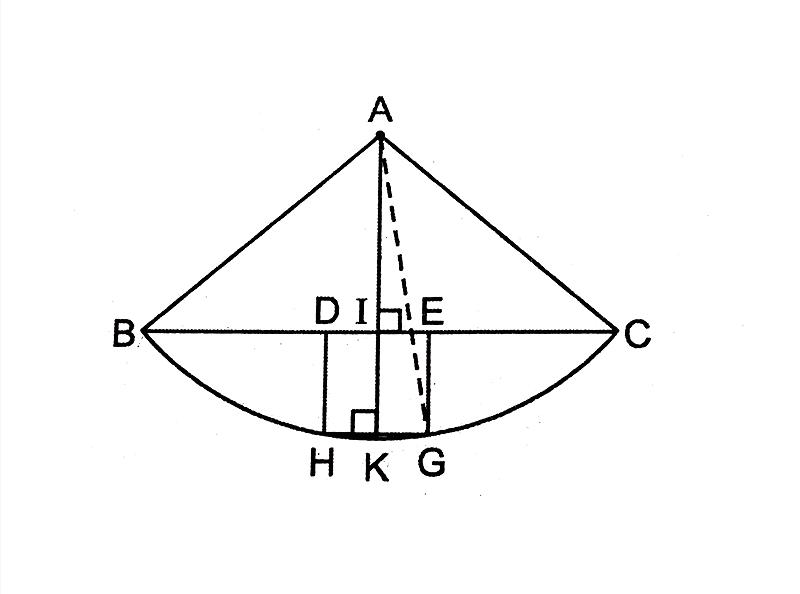
Gọi A là tâm đường tròn chứa cung BC. Ta có BC = a nên:

\(AC=\dfrac{a}{\sqrt2}\).
Ta tính được diện tích của hình viên phân bằng:

\(S=\dfrac{a^2}{8}(\pi -2)\).

Xem thêm: Bài 85 trang 100 SGK Toán 9 tập 2

Dưới đây là một số tips để nắm chắc kiến thức liên quan đến dạng bài tập này:

• Nắm chắc kiến thức nền tảng
• Luyện tập các bài toán về công thức diện tích hình viên phân có sẵn trong sách giáo khoa hoặc sách tham khảo. 
• Tham gia trao đổi trên lớp, làm bài tập nhóm và hỏi ý kiến thầy cô cùng là một phương pháp học rất tốt được nhiều học sinh áp dụng.
• Tìm hiểu thêm các bài giảng dạy, các bài chữa bài tập trên các trang mạng xã hội liên quan đến học tập, ví dụ như Cùng học vui,...

Hy vọng những bài viết về công thức tính diện tích hình viên phân trên sẽ là sự lựa chọn tối ưu và hữu ích cho bạn đọc trong quá trình ôn luyện. Chúng tôi luôn mong muốn cung cấp những thông tin cần thiết nhất một cách ngắn gọc và súc tích để các bạn có thể dễ dàng theo dõi. Mọi ý kiến đóng góp có thể để dưới mục bình luận, chúng tôi sẽ cố gắng khắc phục và hoàn thiện. Cảm ơn sự quan tâm của bạn đọc!