40 bài tập trắc nghiệm hàm số y=ax+b
- Câu 1 : Trong các hàm số sau, hàm số bậc nhất là :
A \(y = \frac{{2x - 2}}{3}\)
B \(y = \frac{{ - 2}}{{2x + 1}}\)
C \(y = \frac{{mx + 1}}{x}\)
D \(y = \sqrt {mx + x} \)
- Câu 2 : Số các giá trị nguyên của \(m\) trong đoạn \(\left[ { - 2018;2018} \right]\) để hàm số \(f\left( x \right) = \left( {m + 1} \right)x + m - 2\) đồng biến trên \(\mathbb{R}\) là:
A \(2019\)
B \(4037\)
C \(4036\)
D \(2018\)
- Câu 3 : Cho hàm số \(y = 2mx - m - 1\,\,\,\left( d \right)\). Tìm m để đường thẳng (d) đi qua điểm \(A\left( {1;\,\,2} \right)\).
A \(m < 3\)
B \(m = - 3\)
C \(m=3\)
D Không tồn tại
- Câu 4 : Tìm các giá trị của m để hàm số \(y = \left( {{m^2} - m} \right)x + 1\) đồng biến trên R.
A \(0 < m < 1\)
B \(m \in \left( { - \infty ;\,\,0} \right) \cup \left( {1;\,\, + \infty } \right)\)
C \(\left[ \matrix{ m = 0 \hfill \cr m = 1 \hfill \cr} \right.\)
D Không tồn tại
- Câu 5 : Đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {0; - 3} \right);\,B\left( { - 1; - 5} \right).\) Thì \(a\) và \(b\) bằng
A \(a = - 2;\,b = 3\)
B \(a = 2;\,b = 3\)
C \(a = 2;\,b = - 3\)
D \(a = 1;\,b = - 4\)
- Câu 6 : Gọi \(S\) là tập các giá trị nguyên của tham số \(m\) để hàm số \(y = \left( {4 - {m^2}} \right)x + 2\) đồng biến trên \(\mathbb{R}.\) Tính số phần tử của \(S.\)
A \(5.\)
B \(2.\)
C \(1.\)
D \(3.\)
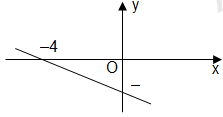
- Câu 7 : Cho hàm số \(y = ax + b\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A \(a > 0,b < 0.\)
B \(a < 0,b < 0.\)
C \(a > 0,b > 0.\)
D \(a < 0,b > 0.\)
- Câu 8 : Cho hàm số \(y = f\left( x \right)\) có tập xác định là \(\left[ { - 3;3} \right]\) và có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
B Hàm số đồng biến trên khoảng \(\left( { - 3;1} \right)\) và \(\left( {1;4} \right)\).
C Hàm số nghịch biến trên khoảng \(\left( { - 2;1} \right)\).
D Hàm số đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) và \(\left( {1;3} \right)\).
- Câu 9 : Đồ thị hàm số \(y = x + 1\) đi qua điểm nào sau đây?
A \((0;1).\)
B \((2; - 1).\)
C \((0;2).\)
D \((1;0).\)
- Câu 10 : Hàm số \(f\left( x \right) = \left( {m - 1} \right)x + m + 2\) (với \(m\) là tham số thực) nghịch biến trên \(\mathbb{R}\) khi và chỉ khi
A \(m \ge 1\)
B \(m < 1\)
C \(m > 1\)
D \(m \le 1\)
- Câu 11 : Tìm tất cả các giá trị của \(m\)để hàm số \(y = \left( {2m - 1} \right)x + m - 3\) đồng biến trên \(\mathbb{R}.\)
A \(m < \frac{1}{2}.\)
B \(m > \frac{1}{2}.\)
C \(m < 3.\)
D \(m > 3.\)
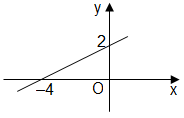
- Câu 12 : Hình vẽ sau đây là đồ thị của hàm số nào?
A \(y = x - 2\)
B \(y = - x - 2\)
C \(y = - 2{\rm{x}} - 2\)
D \(y = 2{\rm{x}} - 2\)
- Câu 13 : Biểu thức \(f\left( x \right) = 3x + 5\) nhận giá trị dương khi và chỉ khi:
A \(x < - \frac{5}{3}\)
B \(x \ge - \frac{5}{3}\)
C \(x > - \frac{5}{3}\)
D \(x > \frac{5}{3}\)
- Câu 14 : Điểm nào dưới đây không thuộc đồ thị hàm số \(y = - 4x + 6\).
A \(N\left( {1;2} \right)\)
B \(M\left( {2;2} \right)\)
C \(P\left( {3; - 6} \right)\)
D \(Q\left( { - 3;18} \right)\)
- Câu 15 : Với giá trị nào của m thì hàm số \(y = \left( {2 - 3m} \right)x + m + 1\) nghịch biến trên tập xác định của nó.
A \(m \ge \frac{2}{3}\)
B \(m > \frac{2}{3}\)
C \(m < \frac{3}{2}\)
D \(m < \frac{2}{3}\)
- Câu 16 : Cho hai đường thẳng \({d_1}:y = x + 100\) và \({d_2}:y = \frac{1}{2}x + 100.\) Mệnh đề nào sau đây đúng?
A \({d_1}\) và \({d_2}\) trùng nhau.
B \({d_1}\) và \({d_2}\) cắt nhưng không vuông góc
C \({d_1}\) và \({d_2}\) song song với nhau.
D \({d_1}\) và \({d_2}\) vuông góc.
- Câu 17 : Phương trình đường thẳng \(y = ax + b\) đi qua hai điểm \(A\left( { - 1;2} \right)\) và \(B\left( {3;1} \right)\) là ?
A \(y = - \frac{x}{4} + \frac{7}{4}\)
B \(y = \frac{x}{4} + \frac{7}{4}\)
C \(y = \frac{{3{\rm{x}}}}{2} + \frac{7}{2}\)
D \(y = - \frac{{3{\rm{x}}}}{2} + \frac{1}{2}\)
- Câu 18 : Tìm tất cả các giá trị thực của tham số \(m\) để đường thẳng \(y = 3x + 1\) song song với đường thẳng \(y = \left( {{m^2} - 1} \right)x + \left( {m - 1} \right).\)
A \(m = \pm 2\)
B \(m = 2\)
C \(m = - 2\)
D \(m = 0\)
- Câu 19 : Tìm \(m\) để 3 đường thẳng \({d_1}:y = x + 1,{d_2}:y = 3x - 1,{d_3}:y = 2mx - 4m\) đồng quy (cùng đi qua một điểm)?
A \(m = 0\)
B \(m = - 1\)
C \(m = 1\)
D \(m \in \emptyset \)
- Câu 20 : Đồ thị hình bên là của hàm số nào sau đây?
A \(y = \left\{ {\begin{array}{*{20}{c}}{2x - 3{\rm{\,\,\,\, khi \,\,\,\,}}x \ge 1}\\{x - 2\,{\rm{\,\,\,\,khi \,\,\,\,}}x < 1}\end{array}} \right.\)
B \(y = \left\{ {\begin{array}{*{20}{c}}{x - 2{\rm{\,\,\,\, khi\,\,\,\, }}x \ge 1}\\{2x - 3{\rm{\,\,\,\, khi \,\,\,\,}}x < 1}\end{array}} \right.\)
C \(y = \left\{ {\begin{array}{*{20}{c}}{3x - 4{\rm{\,\,\,\, khi\,\,\,\,}}x \ge 1}\\{ - x{\rm{\,\,\,\, khi\,\,\,\, }}x < 1}\end{array}} \right.\)
D \(y = \left| {x - 2} \right|\)
- Câu 21 : Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho sau đây ?
A \(y = 2x - 1\)
B \(y = \left| {2{\rm{x}} - 1} \right|\)
C \(y = 1 - 2x\)
D \(y = - \left| {2x - 1} \right|\)
- Câu 22 : Biết đồ thị hàm số \(y = ax + b{\rm{ }}\left( {a \ne 0} \right)\) đi qua điểm \(N\left( {4; - 1} \right)\) và vuông góc với đường thẳng \(4x - y + 1 = 0.\) Tính tích \(P = ab.\)
A \(P = 0\)
B \(P = - \frac{1}{4}\)
C \(P = \frac{1}{4}\)
D \(P = - \frac{1}{2}\)
- Câu 23 : Đồ thị của hàm số y = \( - \frac{x}{2} + 2\) là hình nào ?
A
B
C
D
- Câu 24 : Tìm hai số thực \(a,\;b\;\)để đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A(1;2)\) và \(B( - 2;4)\).
A \(a = \frac{5}{2}\) và \(b = - \frac{3}{4}\).
B \(a = - \frac{4}{3}\) và \(b = \frac{{10}}{3}\).
C \(a = - \frac{3}{2}\) và \(b = 4\).
D \(a = - \frac{2}{3}\) và \(b = \frac{8}{3}\).
- Câu 25 : Điểm A có hoành độ \({x_A} = 1\) và thuộc đồ thị hàm số \(y = mx + 2m - 3\). Tìm m để điểm A nằm trong nửa mặt phẳng tọa độ phía trên trục hoành (không chứa trục hoành).
A \(m < 0\)
B \(m > 0\)
C \(m \le 1\)
D \(m > 1\)
- Câu 26 : Trong các hàm số sau, hàm số nào tăng trên khoảng \(\left( { - 1;0} \right)\).
A
\(y = x\)
B \(y = \left| x \right|\)
C \(y = {x^2}\)
D \(y = \frac{1}{x}\).
- Câu 27 : Cho hàm số \(y = \left| {x - 3} \right|\). Chọn khẳng định đúng trong các khẳng định sau về hàm số
A Hàm số chẵn
B Hàm số đồng biến trên R
C Giá trị nhỏ nhất của hàm số là \(y = 0\)
D Hàm số nghịch biến trên R.
- Câu 28 : Tìm m để 3 đường thẳng \({d_1}:\,\,y = x + 1;\,\,{d_2}:\,\,y = 3x - 1;\,\,{d_3}:\,\,2mx - 4m\) đồng quy (cùng đi qua 1 điểm) ? Đáp án đúng là:
A \(m = 1\)
B \(m = - 1\)
C \(m = 0\)
D \(m \in \emptyset \)
- Câu 29 : Tọa độ giao điểm của (d1): y = 3x và (d2):y= x-3
A
\(\left( {2;6} \right)\)
B
\(\left( {\frac{3}{2}; - \frac{9}{2}} \right)\)
C
\(\left( { - \frac{3}{2};\frac{9}{2}} \right)\)
D \(\left( { - \frac{3}{2}; - \frac{9}{2}} \right)\)
- Câu 30 : Hàm số\(y = \left| {2x + 10} \right|\) là hàm số nào sau đây:
A \(y = \left\{ \begin{array}{l}2x + 10,...x \ge - 5\\2x - 10,...x < - 5\end{array} \right.\)
B \(y = \left\{ \begin{array}{l}2x + 10,...x \ge - 5\\ - 2x + 10,...x < - 5\end{array} \right.\)
C \(y = \left\{ \begin{array}{l}2x + 10,...x \ge 5\\ - 2x - 10,...x < 5\end{array} \right.\)
D \(y = \left\{ \begin{array}{l}2x + 10,...x \ge - 5\\ - 2x - 10,...x < - 5\end{array} \right.\)
- Câu 31 : Cho hàm số \(y = x - 1\) có đồ thị là đường thẳng \(\Delta \). Đường thẳng \(\Delta \) tạo với hai trục toạ độ một tam giác có diện tích \(S\) bằng bao nhiêu?
A \(S = \frac{1}{2}\)
B \(S = 1\)
C \(S = 2\)
D \(S = \frac{3}{2}\)
- Câu 32 : Cho hàm số bậc nhất \(y = ax + b\,\,\,\left( {a \ne 0} \right).\) Tìm \(a\) và \(b\), biết rằng đồ thị hàm số cắt đường thẳng \({\Delta _1}:y = 2x + 5\) tại điểm có hoành độ là \( - 2\) và cắt đường thẳng \({\Delta _2}:y = - 3x + 4\) tại điểm có tung độ là \( - 2.\)
A \(a = \frac{3}{4};b = \frac{1}{2}\)
B \(a = - \frac{3}{4};b = \frac{1}{2}\)
C \(a = - \frac{3}{4};b = - \frac{1}{2}\)
D \(a = \frac{3}{4};b = - \frac{1}{2}\)
- Câu 33 : Cho đường thẳng \(d:\frac{x}{a} + \frac{y}{b} = 1,{\rm{ }}\left( {a \ne 0,\,\,\,b \ne 0} \right)\) đi qua điểm \(M\left( { - 1;6} \right)\) tạo với các tia \(Ox,Oy\) một tam giác có diện tích bằng 4. Tính \(S = a + 2b.\)
A \(S = \frac{{ - 38}}{3}.\)
B \(S = \frac{{ - 5 + 7\sqrt 7 }}{3}.\)
C \(S = 6.\)
D \(S = 12.\)
- Câu 34 : Tìm phương trình đường thẳng \(d:y = ax + b.\) Biết đường thẳng \(d\) đi qua điểm \(I\left( {1;3} \right)\), cắt hai tia \(Ox,{\rm{ }}Oy\) và cách gốc toạ độ một khoảng bằng \(\sqrt 5 .\)
A \(y = 2x + 5.\)
B \(y = - 2x - 5\)
C \(y = 2x - 5\)
D \(y = - 2x + 5\)
- Câu 35 : Tìm các giá trị thực của \(m\) để ba đường thẳng \(y = - 5\left( {x + 1} \right),{\rm{ }}y = mx + 3\) và \(y = 3x + m\) không trùng nhau và cắt nhau tại một điểm.
A \(m = - 13\)
B \(m = 13\)
C \(m = 5\)
D \(m = - 5\)
- Câu 36 : Tìm \(m\) để đường thẳng \(y = m\) cắt đồ thị của hàm số \(y = \frac{{\sqrt {{x^2} + 4x + 4} }}{{x + 2}} - \left| {x - 2} \right|\) tại hai điểm phân biệt?
A \( - 5 < m < - 3\)
B \(\left[ \begin{array}{l}m < - 5\\m > - 3\end{array} \right.\)
C \(m = 1\)
D \(m > 1\)
- Câu 37 : Với giá trị nào của \(m\) thì giá trị lớn nhất của \(f\left( x \right) = \left| {2x - m} \right|\) trên \(\left[ {1;2} \right]\) đạt giá trị nhỏ nhất?
A \(2\)
B \(3\)
C \(4\)
D \(5\)
- Câu 38 : Xác định hàm số bậc nhất \(y = ax + b,\) biết đồ thị hàm số của nó cắt \(Ox,Oy\) lần lượt tại \(A\) và \(B\) sao cho tam giác \(OAB\) cân và qua điểm \(M\left( {2;1} \right).\)
A \(\left[ \begin{array}{l}y = - 2x + 2\\y = x - 2\end{array} \right..\)
B \(\left[ \begin{array}{l}y = - x + 3\\y = x - 1\end{array} \right..\)
C \(\left[ \begin{array}{l}y = - \frac{1}{2}x + 2\\y = \frac{1}{2}x\end{array} \right..\)
D \(\left[ \begin{array}{l}y = - 2x + 5\\y = 2x - 3\end{array} \right..\)
- - Trắc nghiệm Hình học 10 Bài 1 Các định nghĩa
- - Trắc nghiệm Hình học 10 Bài 2 Tổng và hiệu của hai vectơ
- - Trắc nghiệm Hình học 10 Bài 3 Tích của vectơ với một số
- - Trắc nghiệm Hình học 10 Bài 4 Hệ trục tọa độ
- - Trắc nghiệm Ôn tập chương Vectơ - Hình học 10
- - Trắc nghiệm Hình học 10 Bài 1 Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- - Trắc nghiệm Hình học 10 Bài 2 Tích vô hướng của hai vectơ
- - Trắc nghiệm Hình học 10 Bài 3 Các hệ thức lượng trong tam giác và giải tam giác
- - Trắc nghiệm Ôn tập chương Tích vô hướng của hai vectơ và ứng dụng - Hình học 10
- - Trắc nghiệm Toán 10 Bài 1 Mệnh đề