Tổng hợp lý thuyết tính diện tích hình thoi và bài tập chứng minh

Ngay từ tiểu học thì các bạn học sinh đã được làm quen về hình thoi nhưng ở mức độ kiến còn cơ bản. Khi lên trung học, phổ thông thì kiến thức được nâng cao hơn đòi hỏi các bạn cũng cần có nhiều phương pháp và kiến thức để giải quyết các bài toán liên quan. Vậy các bạn học sinh có đang gặp vấn đề về cách tính diện tích hình thoi và những cách chứng minh hình thoi thì hi vọng đây sẽ là bài viết hữu ich mà giúp đỡ được các bạn những khó khăn trong việc tìm kiếm những lời giải

I. Định nghĩa

Hình thoi là tứ giác có bốn cạnh bằng nhau.

II. Tính chất hình thoi

Trong hình thoi:

1. Các góc đối nhau bằng nhau.
2. Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
3. Hai đường chéo là các đường phân giác của các góc của hình thoi.
4. Hình thoi có tất cả tính chất của hình bình hành

III. Dấu hiệu nhận biết hình thoi

Hình tứ giác đặc biệt

• Tứ giác có bốn cạnh bằng nhau là hình thoi.

• Tứ giác có 2 đường chéo là đường trung trực của nhau là hình thoi.
• Tứ giác có 2 đường chéo là đường phân giác của cả bốn góc là hình thoi.

Hình bình hành đặc biệt

Hình thoi là một dạng đặc biệt của một hình bình hành vì nó có đầy đủ tính chất của hình bình hành và còn có một số tính chất khác:

1. Hình bình hành có hai cạnh bên bằng nhau là hình thoi.
2. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
3. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

IV. Công thức tính diện tích hình thoi

Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo:

\({\displaystyle S={\frac {1}{2}}(d_{1}\times d_{2})}\)

Bên cạnh công thức tính diện tích thì các bạn có thể tham khảo thêm cách tính chu vi hình thoi bằng độ dài một cạnh nhân với 4:

\({\displaystyle P={a\times 4}}\)

V. Cách chứng minh hình thoi

Có 4 cách để chứng minh hình thoi

1. Tứ giác có 4 cạnh bằng nhau.

2. Hình bình hành có hai cạnh kề bằng nhau.

3. Hình bình hành có hai đường chéo vuông góc với nhau.

4. Hình bình hành có một đường chéo là tia phân giác của một góc.

VI. Một số bài tập mẫu và phương pháp giải

1. Bài tập và lời giải

 

Bài 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.

 

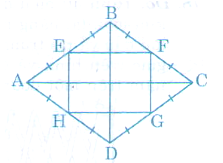
Ta có: EB = EA, FB = FA (giả thiết )

Nên EF là đường trung bình của ΔABC.

Do đó EF // AC

HD = HA, GD = GC (giả thiết) nên HG là đường trung bình của ΔADC.

Do đó HG // AC

Suy ra EF // HG (1)

Chứng minh tương tự EH // FG (2)

Từ (1) và (2) ta được EFGH là hình bình hành

Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF

EH // BD và EF ⊥ BD nên EF ⊥ EH

Nên∠FEH=90∘∠FEH=90∘

Hình bình hành EFGH có góc E = 90o nên là hình chữ nhật

Bài 5: Chứng minh rằng:

a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.

b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

Lời giải:

a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng.

Hình thoi cũng là một hình bình hành nên giao điểm của hai đường chéo hình thoi là tâm đối xứng của hình.

b) 

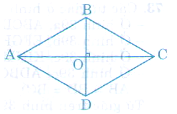
- BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.

- Mọi điểm trên BD đều đối xứng qua chính đường thẳng BD. (*)

- Tâm O là tâm đối xứng mà O ∈ BD

=> BD là trục đối xứng của hình thoi. (**)

- Tương tự AC cũng là là trục đối xứng của hình thoi.

((*) Điểm đối xứng của điểm B qua BD chính là điểm B.

(**) Định nghĩa trục đối xứng: Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.)

2. Một số cách làm bài tập có liên quan đến tính diện tích hình thoi

Tính diện tích hình thoi không phải là dạng bài tập khó. Nhưng với bất cứ một dạng bài nào thì cũng cần các bạn học sinh phải có một sự chăm chỉ và tập trung nhất định. Để làm được những bài tập về hình thoi ngoài việc nắm được hình thoi như thế nào, những cách nhận biết hình thoi và chứng minh hình thoi thì việc tiếp theo là các bạn hãy chăm chỉ làm bài tập. Và sau đây là một số lời giải mà các bạn nên tham khảo để nắm chắc kiến thức về hình thoi

Bài 73 trang 105 SGK Toán 8 tập 1

Bài 84 trang 109 SGK Toán 8 tập 1

Bài 34 trang 128 SGK toán 8 tập 1

Bài 36 trang 129 SGK Toán 8 tập 1

Bài 87 trang 111 SGK toán 8 tập 1

Bài 33 trang 128 SGK Toán 8 tập 1

Hi vọng rằng những công thức cũng như lý thuyết tính diện tích hình thoi mà chúng tôi cung cấp đến cho các học sinh, mong rằng sẽ giúp ích được thật nhiều cho các bạn trong việc làm bài tập. Trong quá trình còn nhiều sai xót rất mong nhận được ý kiến đóng góp từ các bạn để chúng tôi hoàn thiện bài viết của mình hơn. Chúc các bạn đạt kết quả cao trong học tập