Thể tích hình nón cụt, diện tích xung quanh và diện tích toàn phần
Thể tích hình nón cụt, diện tích xung quanh và diện tích toàn phần
Bài học hôm nay chúng ta sẽ tìm hiểu về các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón cụt cùng phương pháp giải các dạng toán thường gặp. Nếu bạn đang thắc mắc về dạng toán này thì bài viết chắc chắn sẽ là sự lựa chọn thích hợp cho bạn. Mời bạn cũng khám phá!
I. Định nghĩa
Hình nón cụt là hình được tạo ra từ hình nón như sau: cho tam giác AOC vuông ở O. Khi quay tam giác vuông này một vòng quanh cạnh OA ta sẽ được một hình nón. Cạnh OC quét đáy tạo thành một hình tròn tâm O bán kính OC. Trong khi đó, cạnh AC quét tạo thành mặt xung quanh của hình nón và cạnh AC được gọi là đường sinh của hình nón.
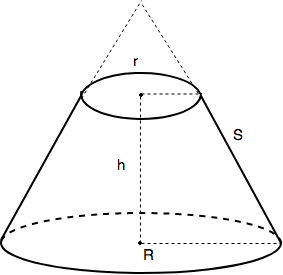
II. Công thức liên quan đến tính diện tích hình nón cụt
Diện tích xung quanh hình nón cụt
\(S_{xq}=\pi (r_1+r_2)l\)
Diện tích toàn phần hình nón cụt
\(S_{tp}=\pi (r_1+r_2)l+\pi r_1^2+\pi r_2^2\)
Diện tích hình nón cụt được tính theo công thức sau:
\(A=\pi(R+r)s=\pi(R+r)\sqrt{h^2+(R-r)^2}\)
Xem thêm tại: Công thức tính diện tích và thể tích hình nón cụt
III. Công thức tính thể tích hình nón cụt
\(V=\dfrac{1}{3} \pi h(R^2+r^2+Rr)\)
Muốn tính thể tích nón cụt các bạn phải tìm được độ dài chiều cao vuông góc với hai đáy và độ dài 2 bán kính của mặt đáy lớn và đáy bé.
Mọi người cũng tìm kiếm:
IV. Bài tập mẫu có lời giải
Bài 1:
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy a,b (a
Bài giải:
Ta có hai tam giác vuông AO’C và AOB đồng dạng vì có góc chung.
Nên: \(\Rightarrow \dfrac{l_1}{l-l_1}=\dfrac{a}{b}\Rightarrow l_1=\dfrac{a}{b}l-\dfrac{a}{b}l_1\)
\(\Rightarrow (1+\dfrac{a}{b})l_1=\dfrac{a}{b}l\Rightarrow l_1=\dfrac{a}{a+b}l\)
Diện tích xung quanh của hình nón lớn:
S(xq nón lớn) = \(\pi.r.l=\pi.b.l\)
Diện tích xung quang của hình nón nhỏ:
S(xp nón nhỏ) = \(\pi .r.l+1=\pi.a.\dfrac{a}{a+b}l=\pi \dfrac{a^2}{a+b}l\)
Diện tích xung quanh hình nón cụt:
S(xq nón cụt) = S(xq nón lớn) - S(xp nón nhỏ)
\(= \pi.b.l - \pi \dfrac{a^2}{a+b}l= (\dfrac{b^2+ab-a^2}{a+b})\pi l\)
Bài 2:
Một xô bằng inốc có dạng nón cụt đựng hóa chất, có các kích thước bán kích đáy lớn là 21 cm và bán kính đáy nhỏ là 9 cm. Độ dài đường sinh là 36 cm.
a) Hãy tính diện tích xung quanh của xô.
b) Khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu.
Lời giải:
a) Diện tích cần tính gồm diện tích xung quanh của hình xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính 9cm. Đường sinh của hình nón lớn là l = 36 + 27 = 63 cm.
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:
Sxq nón lớn = πrl = 3,14.21.63 = 4154,22 (cm2)
Sxq nón nhỏ = 3,14.9.27 = 763,02 (cm2)
Diện tích xung quanh của hình nón cụt:
Sxq nón cụt = Sxq nón lớn - Sxq nón nhỏ = 4154,22–763,02 = 3391,2 (cm2)
Diện tích hình tròn đáy:
S hình tròn đáy = 3,14.92^2 = 254,34 (cm2)
Diện tích mặt ngoài của xô:
S = Sxq nón cụt + S hình tròn đáy
= 3391,2 + 254,34
= 3645,54 (cm2)
b) Chiều cao của hình nón lớn:
\(h=\sqrt{63^2+21^2}=59,397 (cm)\)
Chiều cao của hình nón nhỏ:
\(h'=\sqrt{27^2+9^2}=25,546 (cm)\)
Thể tích của hình nón lớn:
V hình tròn lớn\(= \dfrac{1}{3}\pi rh= \dfrac{1}{3}.3,14.21^2.59,397=27416,467(cm^3)\)
Thể tích của hình nón nhỏ:
V hình tròn nhỏ\(= \dfrac{1}{3}\pi rh= \dfrac{1}{3}.3,14.9^2.25,456=2158,160(cm^3)\)
Khi xô chứa đầu hóa chất thì dung tích của nó là:
V = V hình tròn lớn - V hình tròn nhỏ
= 27416,467 - 2158,160 = 25258 (cm3)
Xem ngay:
- Giải bài 18 trang 117 - Sách giáo khoa Toán 9 tập 2
- Giải bài 28 trang 120 - Sách giáo khoa Toán 9 tập 2
Bài tập trắc nghiệm:
Câu 1: Một hình nón có bán kính đáy là 5cm, đường sinh bằng 13cm. Thể tích hình nón đã cho là:
A. \(50π(cm^3)\)
B. \(100π(cm^3)\)
C. \(200π(cm^3)\)
D. \(150π(cm^3)\)
Câu 2: Hình ABCD khi quay quanh cạnh BC, ta tạo ra được:
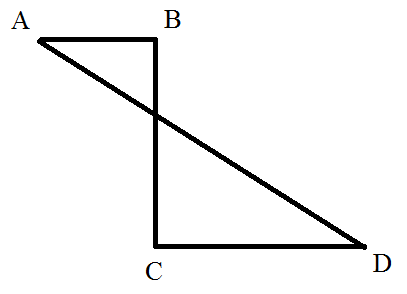
A. Một hình trụ
B. Một hình nón
C. Một hình nón cụt
D. Hai hình nón
Câu 3: Diện tích xung quanh của hình nón cụt có bán kính đáy lớn đáy nhỏ lần lượt là 15cm,8cm và có đường sinh bằng 10cm là:
A. \(70π(cm^2)\)
B. \(230π(cm^2)\)
C. \(12π(cm^2)\)
D. \(1200π(cm^2)\)
Chúng tôi vui lòng cung cấp tới bạn đọc bộ công thức tính hình nón cụt bao gồm có công thức tính diện tích xung quanh, diện tích toàn phần và thể tích hình nón cụt. Với các công thức tổng hợp nêu trên hi vọng các bạn sẽ hiểu và áp dụng tính thể tích hình nón cụt một cách chuẩn nhất. Chúc các bạn thành công!

