Lý 10 Lực hấp dẫn định luật vạn vật hấp dẫn

Lý 10 Lực hấp dẫn định luật vạn vật hấp dẫn

Trong bài viết này Cunghocvui sẽ giới thiệu tới các bạn một nội dung học rất quan trọng và bổ ích về lý thuyết lực hấp dẫn định luật vạn vật hấp dẫn!

I. Lý thuyết

1. Lý thuyết hấp dẫn của Newton

Định luật hấp dẫn do nhà vật lý học Newton khám phá ra được phát biểu như sau: Một vật có khối lượng nhất định làm sẽ bị một lực tác động vào nếu để gần một vật có khối lượng M, m sẽ bị kéo gần lại m với một gia tốc xác định g. Lực đó là lực hấp dẫn. Công thức định luật như sau:

\({\displaystyle g={\frac {GM}{d^{2}}}}\)

Với:

• Hằng số hấp dẫn là G
• Hai vật đặt cách nhau một khoảng xác định là dlam

Khi xác định được gia tốc kéo vật, ta sẽ suy ra công thức tính độ lớn của lực như sau:

\(F = m g\)

\({\displaystyle F={\frac {GMm}{d^{2}}}}\)

Từ công thức nêu trên ta có thể rút ra được nguyên tắc nhất quán, lực có chịu tác động cùng chiều so với khối lượng của hai vật quan sát, và chịu tác động nghịch so với vật gia tốc g. Kích thước được xác định là rất nhỏ so với khoảng cách tương đối giữa hai vật quan sát.

2. Hằng số hấp dẫn

Khi xuất hiện một lực hấp dẫn hình thành bởi hai vật ta sẽ hoàn toàn tính được một hằng số quy chuẩn gọi là hằng số hấp dẫn, xác định bởi kết quả của các cuộc thí nghiệm, ta có giá trị hằng số xác định được như sau:

\(G = 6.67 \times 10^{−11} N.m²/kg²\)

3. Trọng lực

Một vật bất kỳ nằm trên phạm vi xác định của trái đất đều bị chịu tác động bởi trọng lực. Trọng lực có xu hướng hút vật về tâm của Trái Đất. Nếu thiếu trọng lực vật sẽ bị bay lơ lửng trong không trung. Ta có công thức xác định trọng lực tác động lên vật như sau:

\({\displaystyle F={\frac {GMm}{d^{2}}}}\)

• Hằng số hấp dẫn là G
• Hai vật đặt cách nhau một khoảng xác định là d
• m: Khối lượng vật nghiên cứu

4. Trọng lực tiêu chuẩn

Tiêu chuẩn là khi ta xác định được trọng lực tác động vào vật ở một khoảng tương đối được chấp nhận, gia tốc áp dụng vào vật được ký hiệu là \(g_o \ hay \ g_n\) được xác định dựa vào độ cao tương quan so với mực nước biển.

5. Thế năng hấp dẫn

Tỷ lệ nghịch so với bình phương vecto bảo toàn của vật. Thế năng có giá trị khi vật được xét cách mặt đất một khoảng d tạo ra thế năng hấp dẫn tương quan chỉ sự tác động của lực hướng tâm lên vật. Một vật ở điều kiện thường đều chịu tác động của thế năng. Chính vì vậy cho dù là tác động từ các hướng khác nhau đến vật và khoảng cách là từ vị trí r0 đến r đều chịu chung một lực quán tính được xác định như sau:

\({\displaystyle \int _{\mathbf {r} _{0}}^{\mathbf {r} }\mathbf {F} \cdot d\mathbf {r} '}\)

Lực không phụ thuộc vào vị trí của khoảng cách xem xét.

Công thức chung cho thế năng hấp dẫn giữa hai chủ thể được đặt cách nhau một khoảng cách d như sau:

\({\displaystyle \phi (\mathbf {r} )=\phi (\mathbf {r} _{0})+\int _{\mathbf {r} _{0}}^{\mathbf {r} }\mathbf {F} \cdot d\mathbf {r} '}\)

6. Định luật vạn vật hấp dẫn

Được nhà vật lý học Albert Einstein khám phá ra bản chất của vạn vật khi tồn tại trên Trái Đất đều chịu tác động từ trường của một lực hướng vào tập, nó có thể là sự uốn cong xuyên không gian và thời gian, chịu tác động bởi nội lực lẫn ngoại lực và các nhân tố xúc tác về mặt bản chất của vật chất và năng lượng.

Lực hấp dẫn - Định luật vạn vật hấp dẫn

II. Các bài tập Lực hấp dẫn định luật vạn vật hấp dẫn

Bài 1: Hai tàu nằm cách nhau 1km có khối lượng tương đương nhau đều bằng 50000 tấn. Tính lực hấp dẫn giữa hai con tàu được xét.

Hướng dẫn:

Đổi:\( 50000 tấn = 5.10^7 kg, 1 km = 1000 m\)

Áp dụng công thức ta có:

\(F_{hd}=G\dfrac{M_1M_2}{r^2}=6.67.10^{-11}.\dfrac{(5.10^7)^2}{1000^2}=0.167 N\)

Bài 2: Xét đến mối tương quan giữa hai vật là mặt trăng và mặt trời, ta nhận thấy khối lượng của mặt trăng nhỏ hơn rất nhiều so với Trái Đất. Theo như kết quả đo được Trái Đất gấp 81 lần so với mặt trăng. Lực tương quan giữa chúng là bao nhiêu, biết rằng bán kính đo được của mặt trăng là R thì của Trái đất sẽ là 60R và lực tương tác là lực hướng tâm nằm trên đường thẳng nối tâm?

Hướng dẫn:

Tham số hóa các chỉ tiêu ta có khối lượng của mặt trăng thì suy ra theo giả thuyết khối lượng của Trái Đất phải là 81M.

Gọi R là bán kính Trái Đất và r sẽ là bán kính của mặt trăng, thoe bài ta có khoảng cách d là khoảng cách của đường nối tâm giữa hai chủ thể ta có d = 60R.

Vật được đặt tương quan giữa mặt trăng và Trái Đất là m, khi đó khoảng cách h là giữa vật m so với Trái Đất và khoảng cách từ m đến Mặt Trăng được suy ra là 60R - h ( điều kiện cho các chỉ số quan trọng là R, h > 0)

Trong không trung lực hấp dẫn giữa các chủ thể cho dù khối lượng có thể khác nhau nhưng lực tác dụng là tương đương nhau. Từ kết luận đó ra có phương trình:

\(F_{hd_1} = F_{hd_2}\)

\(\Rightarrow \dfrac{G.81.M.m}{h^2}=\dfrac{GMm}{(60R-h)^2} \Rightarrow h=54R\)

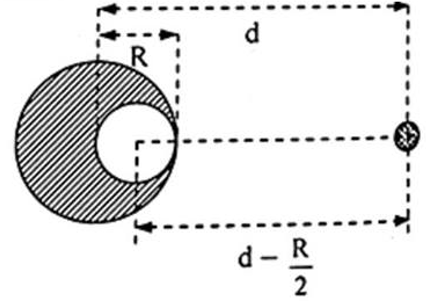
Bài 3: Cho bài toán như hình vẽ dưới đây biết rằng quả cầu có bán kính R được làm đồng chất và ở dạng đặc được đặt trong môi trường tương quan so với một quả cầu nhỏ khối lượng m với khoảng cách đo được giữa hai vật là d. Biết rằng người ta khoét một lỗ nhỏ trong quả cầu đặc có bán kính R/2. Khối lượng ban đầu khi chưa bị khoét là M, yêu cầu tính độ lớn của lực tương quan hấp dẫn giữa hai vật dưới?

Hướng dẫn:

Gọi F1 là lực hấp dẫn giữa quả cầu đã bị khoét với vật m

F2 là lực hấp dẫn giữa quả cầu đã bị khoét đi với vật m

F là lực hấp dẫn giữa quả cầu đã bị khoét đi với vật m

\(F = F_1 + F_2 ⇒ F_1 = F – F_2\)

\(\Rightarrow F_2=G\dfrac{Mm}{d^2}-G\dfrac{m_2m}{(d-\dfrac{R}{2})^2}\)

Vì khối lượng tỉ lệ với thể tích nên ta có:

\(\Rightarrow \dfrac{m_2}{M}=\dfrac{V_2}{V}=\dfrac{(\dfrac{R}{2})^2}{R^3}=\dfrac{1}{8} \Rightarrow 8m_2=M \Rightarrow F_1=GMm[\dfrac{1}{d^2}-\dfrac{1}{8(d-\dfrac{R}{2})^2}]\)

Hy vọng rằng với những kiến thức mới về lý thuyết và giải bài tập Lực hấp dẫn định luật vạn vật hấp dẫn trên đây, các bạn hoàn toàn có thể nắm chắc một cách dễ dàng và có những giờ học thư giãn!