Công thức tính thể tính hình nón và bộ bài tập trắc nghiệm minh họa

Công thức tính thể tính hình nón và bộ bài tập trắc nghiệm minh họa

Bài viết dưới đây chia sẻ đến các bạn khái niệm hình nón, công thức hình nón bao gồm tính thể tích hình nón, tính diện tích xung quanh nón và tính diện tích toàn phần hình nón cùng với ví dụ cụ thể. Nếu các bạn đang tìm kiếm cách tính thể tích hình nón cụt chính xác nhất, vậy mời các bạn hãy cùng tham khảo bài viết dưới đây nhé!

I. Định nghĩa:

1. Hình nón

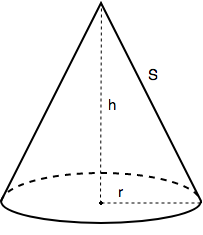
Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.

• Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
• Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
• A là đỉnh và AO là đường cao của hình nón.

2. Hình nón cụt

Được tạo ra từ hình nón như sau: cho tam giác AOC vuông ở O. Khi quay tam giác vuông này một vòng quanh cạnh OA ta sẽ được một hình nón. Cạnh OC quét đáy tạo thành một hình tròn tâm O bán kính OC. Trong khi đó, cạnh AC quét tạo thành mặt xung quanh của hình nón và cạnh AC được gọi là đường sinh của hình nón.

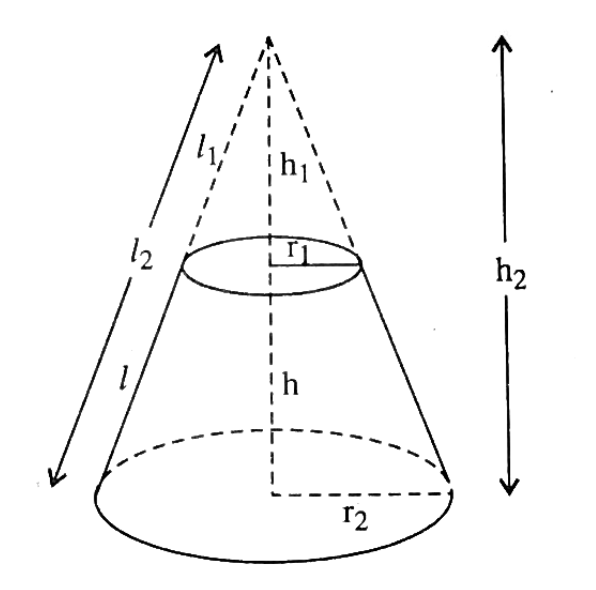
Từ hình nón đã được tạo thành, ta dùng một mặt phẳng song song đáy cắt qua hình nón, ta được một hình nón cụt.

3. Mặt nón.

Cho đường thẳng a. Xét một đường thẳng d cắt a tại O tạo thành một góc a với\(0<\alpha<\dfrac{\pi}{2}\) . Mặt tròn xoay sinh bởi đường thẳng d như thế khi quay quanh a gọi là mặt nón tròn xoay (hay đơn giản hơn là mặt nón).

• a gọi là trục của mặt nón.
• d gọi là đường sinh của mặt nón.
• O gọi là đỉnh của mặt nón.
• Góc 2a gọi là góc ở đỉnh của mặt nón.

4. Khối nón

Một hình nón chia không gian thành hai phần: phần bên trong và phần bên ngoài của nó. Hình nón cùng với phần bên trong của nó gọi là khối nón.

II. Diện tích hình nón

Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của một hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.

• Cách tính diện tích xung quanh hình nón: \(\displaystyle {{S}_{xq}}=2\pi rl\)
• Cách tính diện tích toàn phần hình nón: \(\displaystyle {{S}_{tp}}=\pi rl+\pi r_{{}}^{2}\)
• (r là bán kính đường tròn đáy, l là đường sinh)

Mới nhất: 

• Hình lăng trụ tam giác đầy đủ và chi tiết nhất
• Hình chóp đầy đủ và chi tiết nhất
• Hình trụ tròn đầy đủ và chi tiết nhất

III. Công thức tính thể tích hình nón

1. Thể tích nón

Thể tích của khối nón là giới hạn của thể tích của khối chóp đều nội tiếp khối nón đó khi số cạnh tăng lên vô hạn: V nón = \(\displaystyle \pi r_{{}}^{2}h\)

Tham khảo thêm: Công thức tính diện tích và thể tích hình nón

2. Cách tính thể tích hình nón cụt:

\(V = \dfrac{1}{3}\pi \left( {{r_1}^2 + {r_2}^2 + {r_1}{r_2}} \right)h\)

Trong đó:

• V là thể tích hình nón cụt.
• r1, r2: hai bán kính của hai đáy hình nón cụt.
• h : Chiều cao nối giữa hai đáy của hình nón cụt.
• π: số Pi (3.14159265).

Ví dụ: 

Cho hình nón cụt có đường kính hai mặt đáy lần lượt là 12 cm và 16 cm. Chiều cao nối giữa hai mặt đáy dài 7 cm. Tính thể tích hình nón cụt.

Lời giải:

Đường kính hai mặt đáy lần lượt là 12 cm và 18 cm.

Vậy bán kính đáy \({r_1} = \dfrac{{12}}{2} = 6cm;{r_2} = \dfrac{{18}}{2} = 9cm;h = 7cm\)

\(V = \dfrac{1}{3}\pi \left( {{r_1}^2 + {r_2}^2 + {r_1}{r_2}} \right)h\)

\(\Rightarrow V = \dfrac{1}{3}\pi .\left( {{6^2} + {9^2} + 6.9} \right).7 = \dfrac{1}{3}\pi .\left( {36 + 91 + 57} \right).7 = 1253,5c{m^3}\)

Vậy thể tích hình nón cụt xấp xỉ \( 1253,5c{m^3}\)

IV. Một số câu hỏi trắc nghiệm ôn tập

Câu 1. Một mặt nón tròn xoay có bao nhiêu đường sinh:

A. 1

B. 2

C. 3

D. Vô số.

Câu 2. Khi quay tam giác ABC vuông tại A quanh cạnh AB thì được hình tròn xoay nào?

A. Mặt trụ tròn xoay.

B. Hình trụ tròn xoay.

C. Mặt nón tròn xoay.

D. Hình nón tròn xoay.

Câu 3. Cho tứ diện ABCD có AB vuông góc với (ABC) và BD vuông góc với BC. Khi quay tất cả các cạnh của tứ diện đó quanh AB thì được hình nào?

A. Một hình nón.

B. Một hình trụ.

C. Hai hình nón.

D. Hai hình trụ.

Câu 4. Cho một mặt nón tròn xoay N. Một mặt phẳng (P) cắt mặt nón và song song với một đường sinh duy nhất thì thì giao tuyến của chúng là:

A. Đường tròn.

B. Elip.

C. Parabol.

D. Đường thẳng.

Câu 5. Cho một mặt nón tròn xoay N có trục là D, đỉnh O. Một mặt phẳng (a ) không đi qua O và vuông góc với D sẽ cắt mặt nón N theo một giao tuyến là:

A. Một điểm.

B. Một đường tròn.

C. Một elip.

D. Một parabol.

Đáp án:

1	2	3	4	5
D	D	C	C	B

Bài tập có lời giải:

• Bài 9 trang 52 SGK Hình học 12
• Bài 3 trang 39 SGK Hình học lớp 12

Trên đây bài viết đã chia sẻ đến các bạn khái niệm hình nón, nón cụt và công thức tính thể tích hình nón cụt, cách tính thể tích hình nón cụt với ví dụ cụ thể. Hi vọng các bạn sẽ hiểu và áp dụng tính thể tích hình nón cụt chuẩn nhất. Chúc các bạn thành công!