40 bài tập trắc nghiệm hàm số bậc hai mức độ nhận biết, thông hiểu

Câu 1 : Tọa độ đỉnh của parabol $\left( P \right):\,\,y = - {x^2} + 2x - 3$ là:

A (1;-2)

B (-2;3)

C (-1;2)

D

(2;-3)

Câu 2 : Đồ thị hàm số $y = 3{x^2} + 4x - 1$ nhận đường thẳng nào dưới đây làm trục đối xứng?

$x = \frac{4}{3}$

$y = \frac{2}{3}$

$x = - \frac{2}{3}$

D

$x = - \frac{1}{3}$

Câu 3 : Cho đồ thị $\left( P \right):\,\,y = {x^2} + 4x - 2$ . Điểm nào dưới đây thuộc (P)?

A (1;-3)

B (3;18)

C (-2;-6)

D

(-1;-4)

Câu 4 : Cho hàm số $y = \left( {m - 5} \right){x^2} - 5x + 1$ . Hàm số đã cho là hàm số bậc nhất khi:

$m=5$

$m>5$

$m<5$

$m \ne 5$

Câu 5 : Tìm giao điểm của parabol $\left( P \right):\,\,y = - {x^2} - 2x + 5$ với trục Oy.

A (0;5)

B (5;0)

C (1;4)

D

(0;-5)

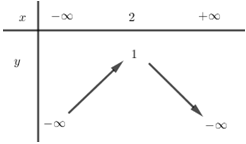
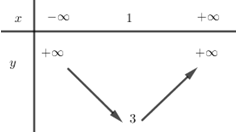
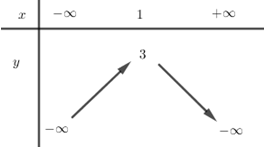
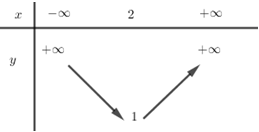
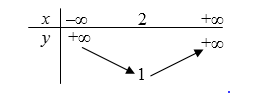
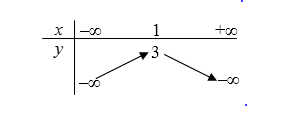
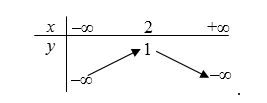
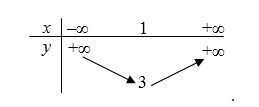
Câu 6 : Bảng biến thiên sau là của hàm số nào?

$y = x{}^2 + 2x - 1.$

$y = {x^2} - 2x + 2.$

$y = 2{x^2} - 4x + 4.$

$y = - 3{x^2} + 6x - 1.$

Câu 7 : Hàm số nghịch biến trên khoảng $\left( { - \infty ;0} \right)$ là

$y = - \sqrt 2 {\left( {x + 1} \right)^2}.$

$y = \sqrt 2 {x^2} + 1.$

$y = - \sqrt 2 {x^2} + 1.$

$y = \sqrt 2 {\left( {x + 1} \right)^2}.$

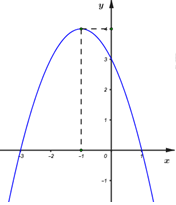
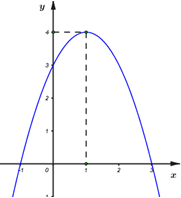
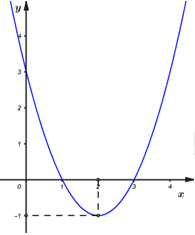
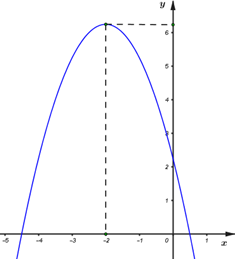
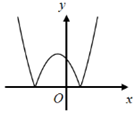
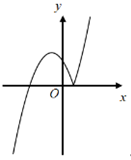
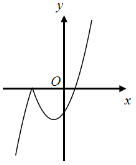
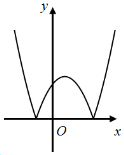
Câu 8 : Hàm số $y = - {x^2} + 2x + 3$ có đồ thị là hình nào trong các hình sau?

A

B

C

D

Câu 9 : Cho hàm số $y = a{x^2} + bx + c\left( {a < 0} \right)$ có đồ thị $\left( P \right)$ . Khẳng định nào sau đây là khẳng định đúng?

Hàm số đồng biến trên khoảng $\left( { - \frac{b}{{2a}}; + \infty } \right)$

Hàm số nghịch biến trên khoảng $\left( { - \infty ; - \frac{b}{{2a}}} \right)$

C Đồ thị luôn cắt trục hoành tại 2 điểm phân biệt.

Đồ thị có trục đối xứng là đường thẳng $x = - \frac{b}{{2a}}$

Câu 10 : Cho parabol $y = f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)$ có bảng biến thiên như hình dưới đây.

$I\left( {5;1} \right).$

$I\left( { - 1; - 5} \right).$

$I\left( { - 1;0} \right).$

$I\left( { - 1;5} \right).$

Câu 11 : Cho hàm số $y = a{x^2} + bx + c$ có đồ thị như hình dưới đây. Mệnh đề nào sau đây đúng?

$a > 0,\,\,\,b = 0,\,\,c > 0$

$a > 0,\,\,b < 0,\,\,\,c > 0$

$a > 0,\,\,b > 0,\,\,c > 0$

$a < 0,\,\,\,b > 0,\,\,\,c > 0$

Câu 12 : Cho parabol $y = a{x^2} + bx + c$ có đồ thị như hình vẽ dưới đây, hỏi mệnh đề nào đúng?

$a > 0,b > 0,c > 0$

$a < 0,b < 0,c < 0$

$a > 0,b > 0,c < 0$

$a < 0,b > 0,c < 0$

Câu 13 : Toạ độ giao điểm của $\left( P \right):y = {x^2} - 4x$ với đường thẳng $y = - x - 2$ là:

$M\left( { - 1; - 1} \right),N\left( {2;0} \right)$

$M\left( {1; - 3} \right),N\left( {2; - 4} \right)$

$M\left( {0; - 2} \right),N\left( {2; - 4} \right)$

$M\left( { - 3;1} \right),N\left( {3; - 5} \right)$

Câu 14 : Giá trị nhỏ nhất của hàm số $y = {x^2} - 4x + 5$ là?

$0$

$- 2$

$2$

$1$

Câu 15 : Cho biểu thức $f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)$ và $\Delta = {b^2} - 4ac$ . Chọn khẳng định đúng.

Khi $\Delta < 0$ thì $f\left( x \right)$ luôn cùng dấu với hệ số a với mọi $x \in \mathbb{R}$

Khi $\Delta = 0$ thì $f\left( x \right)$ trái dấu với hệ số a với mọi $x \ne - \frac{b}{{2a}}$

Khi $\Delta > 0$ thì $f\left( x \right)$ luôn trái dấu với hệ số a với mọi $x \in \mathbb{R}$

Khi $\Delta < 0$ thì $f\left( x \right)$ cùng dấu với hệ số a với mọi $x \ne - \frac{b}{{2a}}$

Câu 16 : Trong các hàm số sau,hàm nào là hàm số bậc 2?

$y = - 2x - 5$

$y = \sqrt {{x^2} + x + 4}$

$y = 4{x^2} - 12x + 9$

$y = \frac{1}{{{x^2} - 2x}}$

Câu 17 : Parabol $y = {x^2} + 1$ nhận điểm nào sau đây làm đỉnh của nó?

$O\left( {0;0} \right)$

$I\left( {1;0} \right)$

$K\left( {0;1} \right)$

$J\left( { - 1;0} \right)$

Câu 18 : Cho parabol $\left( P \right):\,\,y = - 3{x^2} + 9x + 2$ và các điểm $M\left( {2;8} \right);\,\,N\left( {3;56} \right)$ . Chọn khẳng định đúng:

$M \in \left( P \right);\,\,N \in \left( P \right)$

$M \notin \left( P \right);\,\,N \notin \left( P \right)$

$M \notin \left( P \right);\,\,N \in \left( P \right)$

$M \in \left( P \right);\,\,N \notin \left( P \right)$

Câu 19 : Đồ thị trong hình là đồ thị hàm số nào trong các hàm số sau:

$y = {x^2} - 2x + 2$ .

$y = {x^2} + 2x$ .

$y = - {x^2} + 2x$ .

$y = - {x^2} - 2x - 2$ .

Câu 20 : Tìm tất cả các giá trị của tham số m để đồ thị $\left( P \right)$ của hàm số $y = {x^2} + 2x + m - 2$ cắt trục hoành tại hai điểm phân biệt?

$m < 1$

$m > 3$

$m > 1$

$m < 3$

Câu 21 : Tìm điều kiện của các tham số $a,\,\,b,\,\,c$ để hàm số $y = a{x^2} + bx + c$ là hàm số chẵn?

A a tùy ý, b = c = 0

B a, c tùy ý, b = 0

C a, b, c tùy ý

D a, b tùy ý, c = 0

Câu 22 : Xác định hàm số bậc hai $y = a{x^2} - x + c$ biết đồ thị hàm số đi qua A(1;-2) và B(2;3).

$y = 3{x^2} - x - 4$

$y = {x^2} - 3x + 5$

$y = 2{x^2} - x - 3$

D

$y = - {x^2} - 4x + 3$

Câu 23 : Gọi A, B là các giao điểm của đồ thị hàm số $f\left( x \right) = 3{x^2} - 2$ và $g\left( x \right) = 2{x^2} - x + 4$ . Phương trình đường thẳng AB là:

A y = –4x + 9

B y = 3x – 12

C y = –3x + 16

D

y = 4x – 11

Câu 24 : Parabol $\left( P \right):y = a{x^2} + bx + c$ có đồ thị như hình dưới. Tính $M = 4a + 2b - 3c?$

$M = 4.$

$M = 15.$

$M = 7.$

$M = 1.$

Câu 25 : Cho hàm số $y = \left( {x - 1} \right)\left( {x + 2} \right)$ có đồ thị như hinh vẽ bên. Xác định đồ thị của hàm số $y = \left| {\left( {x - 1} \right)\left( {x + 2} \right)} \right|?$

A

B

C

D

Câu 26 : Bảng biến thiên của hàm số $y = 2{x^2} - 4x + 5$ là bảng nào sau đây ?

A

B

C

D

Câu 27 : Cho hàm số $y = 2{x^2} - 4x + 3$ có đồ thị là Parabol $\left( P \right)$ . Mệnh đề nào sau đây sai?

$\left( P \right)$ có trục đối xứng là $d:x = 1$

$\left( P \right)$ có đỉnh là $S\left( { - 1;9} \right)$

$\left( P \right)$ không có giao điểm với trục hoành

$\left( P \right)$ đi qua điểm $M\left( { - 1;9} \right)$

Câu 28 : Hàm số nào trong 4 phương án liệt kê ở A, B, C, D có đồ thị như hình bên ?

$y = {x^2} - 4x + 3$

$y = 2{x^2} + 8x + 3$

$y = {x^2} + 4x + 3$

$y = - {x^2} - 4x + 3$

Câu 29 : Điểm nào sau đây thuộc đồ thị hàm số $y = \left| {2{x^2} - 3} \right|$

$\left( {0; - 3} \right)$

$\left( { - 1; - 1} \right)$

$\left( { - 2;5} \right)$

$\left( { - 2;12} \right)$

Câu 30 : Xác định hàm số bậc hai $y = {x^2} + bx + c,$ biết rằng độ thị hàm số có trục đối xứng là đường thẳng $x = - 2$ và đi qua đi $A\left( {1; - 1} \right).$

$y = {x^2} + 4x - 6.$

$y = {x^2} - 4x + 2.$

$y = {x^2} + 2x - 4.$

$y = {x^2} - 2x + 1.$

Câu 31 : Hàm số nào dưới đây có giá trị lớn nhất bằng $\frac{3}{4}?$

$y = - {x^2} + \frac{3}{2}x + 1.$

$y = {x^2} - 3x + 3.$

$y = - {x^2} + x + \frac{1}{2}.$

$y = - {x^2} + 3x - 3.$

Câu 32 : Đồ thị dưới đây là của hàm số nào?

$y = 2{x^2} - 4x - 1.$

$y = {x^2} - 2x - 1.$

$y = - {x^2} - 2x + 1.$

$y = {x^2} + 2x - 1.$

Câu 33 : Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng $x = 1$ làm trục đối xứng là

$y = - 2{x^2} + 4x + 1.$

$y = 2{x^2} + 4x + 3.$

$y = 2{x^2} - 2x + 1.$

$y = {x^2} - x + 5.$

Câu 34 : Tìm $a$ và $b$ để đồ thị hàm số $y = a{x^2} + bx + 2$ đi qua điểm $A\left( {3;5} \right)$ và có trục đối xứng là đường thẳng $x = 1.$

$a = - 1;b = 2.$

$a = 1;b = - 2.$

$a = \frac{1}{5};b = \frac{2}{5}.$

$a = - \frac{1}{5};b = - \frac{2}{5}.$

Câu 35 : Tìm tập hợp đỉnh $I$ của parabol $y = {x^2} - 2mx + {m^2} + 7m + 2$ ?

Đường thẳng $y = 7x + 2$

Đường thẳng $y = 7x + 3$

Đường thẳng $y = 8x + 5$

Đường thẳng $y = 3x - 1$

Câu 36 : Biết rằng $\left( P \right):y = a{x^2} + bx + 2\,\,\,\left( {a > 1} \right)$ đi qua điểm $M\left( { - 1;6} \right)$ và có tung độ đỉnh bằng $- \frac{1}{4}.$ Tính tích $P = ab.$

$P = - 3$

$P = - 2$

$P = 28$

$P = 192$

Câu 37 : Bảng biến thiên của hàm số $y = - 2{x^2} + 4x + 1$ là bảng nào sau đây?

A

B

C

D

Câu 38 : Tìm tọa độ đỉnh của Parabol $y = 2{x^2} - 4x + 1$ .

$\left( { - 1;7} \right)$ .

$\left( {2;\;1} \right)$ .

$\left( {1; - 1} \right)$ .

$\left( { - 2;\;17} \right)$ $\left( { - 2;\,17} \right)$ .

40 bài tập trắc nghiệm hàm số bậc hai mức độ nhận...