Lực hướng tâm - Vật lí 10

Lực hướng tâm - Vật lí 10

Trong bài viết này Cunghocvui sẽ giới thiệu tới các bạn một nội dung học rất quan trọng và bổ ích về Vật lý 10 Lực hướng tâm!

I. Lý thuyết

1. Lực hướng tâm là gì?

Lực được xác định khi một vật thể bất kỳ chuyển động một quỹ đạo hình tròn và thường có xu hướng bị hút vào tâm. Isaac Newton đã mô tả lực này trong cuốn Principia của ông[2]. Bất kỳ lực nào (trọng lực, lực điện từ, v.v.) hoặc sự kết hợp các lực với nhau đều có thể đóng vai trò là lực hướng tâm. Ta có thể thấy một ví dụ về chuyển động tròn đều trên hình bên phải.

Ví dụ: chuyển động tròn đều

Vectơ vận tốc được định nghĩa là tốc độ của vật cùng với hướng chuyển động. Những vật có tổng lực tác động triệt tiêu sẽ không tăng tốc và do đó di chuyển theo một đường thẳng với tốc độ không đổi; chúng có vận tốc là một hằng số. Tuy nhiên, một vật di chuyển theo đường tròn, mặc dù di chuyển với tốc độ không đổi, vẫn có sự thay đổi hướng chuyển động. Độ thay đổi vectơ vận tốc của vật trong trường hợp này gọi là gia tốc hướng tâm.

Gia tốc hướng tâm khác nhau phụ thuộc vào bán kính cong của quỹ đạo (R) và tốc độ (v) của vật, gia tốc tăng nếu tốc độ tăng hoặc bán kính giảm. Nếu một vật đang di chuyển theo một đường tròn với tốc độ biến thiên, gia tốc của nó có thể được chia thành hai thành phần: gia tốc hướng tâm (gia tốc làm thay đổi hướng vận tốc) và gia tốc tiếp tuyến (gia tốc làm thay đổi độ lớn vận tốc).

2. Độ lớn của lực hướng tâm được cho theo công thức:

\({\displaystyle F={\frac {mv^{2}}{r}}}\)

trong đó m là khối lượng, v là độ lớn vận tốc, và r là bán kính cong của quỹ đạo.

3. Nguồn gốc của lực hướng tâm

Đối với một vệ tinh bay trong quỹ đạo quanh trái đất, lực hướng tâm do lực trọng trường tạo thành giữa vệ tinh và trái đất, và tác dụng lực hướng về khối tâm của hai vật. Đối với một vật được gắn vào đầu một sợi dây đang quay theo trục đứng, lực hướng tâm là thành phần nằm ngang của lực căng dây, tác dụng hướng về tâm khối lượng giữa trục quay và vật quay. Đối với một vật đang xoay quanh chính nó, lực căng bên trong là lực hướng tâm giữ cho vật là một khối.

4. Phân tích một số trường hợp

4.1. Chuyển động tròn đều

Chuyển động tròn đều là trường hợp có độ quay cố định. Dưới đây là hai cách tiếp cận vấn đề.

Phương pháp hình học:

Vectơ vận tốc luôn luôn vuông góc với vectơ vị trí (vì vectơ vận tốc luôn tiếp tuyến với quỹ đạo tròn). Vì R di chuyển theo đường tròn, do đó v cũng vậy. Chuyển động tròn của vận tốc được thể hiện trong đường tròn ở hình bên phải, cùng với gia tốc a. Cũng như vận tốc là mức độ thay đổi vị trí, gia tốc chính là mức độ thay đổi của vận tốc.

- Vì vị trí và vận tốc di chuyển cùng nhau, chúng xoay quanh vòng tròn của chúng với cùng chu kỳ T. Khoảng thời gian đó bằng với khoảng cách đi được chia cho vận tốc.

\({\displaystyle T={\frac {2\pi |\mathbf {R} |}{|\mathbf {v} |}}}\)

và, tương tự,

\({\displaystyle T={\frac {2\pi |\mathbf {v} |}{|\mathbf {a} |}}}\)

- Cho hai phương trình này bằng nhau và giải để tìm |a|, ta có

\({\displaystyle |\mathbf {a} |={\frac {|\mathbf {v} |^{2}}{|\mathbf {R} |}}}\)

- Vận tốc quay tính theo radian trên giây là:

\({\displaystyle \omega ={\frac {2\pi }{T}}\ }\)

Sử dụng vecto

- Mối quan hệ vectơ đối với chuyển động tròn đều, vectơ Q đại diện cho chuyển động quay là vectơ pháp tuyến của mặt phẳng quỹ đạo có chiều được xác định bằng quy tắc bàn tay phải và độ lớn là dθ /dt.
\({\displaystyle |\mathbf {\Omega } |={\frac {\mathrm {d} \theta }{\mathrm {d} t}}=\omega \,} \)

với θ là tọa độ góc vào thời điểm t. Trong phần này, dθ/dt được giả thiết là không thay đổi, không phụ thuộc vào thời gian. Độ dịch chuyển ℓ trong khoảng thời gian vi phân dt trên quỹ đạo tròn là:

\({\displaystyle \mathrm {d} {\boldsymbol {\ell }}=\mathbf {\Omega } \times \mathbf {r} (t)\mathrm {d} t\,}\)

trong đó, theo tính chất của tích có hướng của hai vectơ, có độ lớn bằng rdθ và có phương vuông góc với quỹ đạo.

Công thức Lagrange cho biết:

\({\displaystyle \mathbf {a} \times \left(\mathbf {b} \times \mathbf {c} \right)=\mathbf {b} \times \left(\mathbf {a} \cdot \mathbf {c} \right)-\mathbf {c} \times \left(\mathbf {a} \cdot \mathbf {b} \right)}\)

- Áp dụng công thức Lagrange, để ý rằng Ω • r(t) = 0 tại mọi thời điểm,

\({\displaystyle \mathbf {a} =-{|\mathbf {\Omega |} }^{2}\mathbf {r} (t)}\)

4.2. Chuyển động tròn không đều

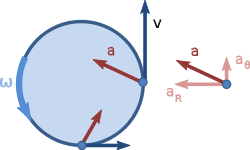
- Gọi r(t) là vector mô tả vị trí khối tâm theo thời gian. Vì chúng ta đang giả sử đây là chuyển động tròn, gọi r(t) = R·ur, trong đó R là hằng số (bán kính của đường tròn) và ur là vectơ đơn vị hưởng từ điểm chuyển động đến khối tâm. Vị trí của ur được mô tả theo θ, góc tạo bởi trục x là vectơ đơn vị, đo theo hướng ngược chiều kim đồng hồ từ trục x.

- Vector đơn vị khác dành cho hệ tọa độ cực, uθ vuông góc với ur và những điểm theo hướng θ tăng dần. Những vector đơn vị cực này có thể được biểu diễn theo vectơ đơn vị Descartes theo phương x và y, ký hiệu lần lượt là i và j:

- Ta có công thức tính gia tốc:\({\displaystyle \mathbf {a} =R\left({\frac {\mathrm {d} \omega }{\mathrm {d} t}}\mathbf {u} _{\mathrm {\theta } }-\omega ^{2}\mathbf {u} _{\mathrm {r} }\right)}\)

- Các phương trình này cho thấy, trong trường hợp một vật di chuyển quanh một đường tròn với tốc độ thay đổi, gia tốc của vật có thể phân thành một thành phần trực giao làm thay đổi hướng chuyển động (gia tốc hướng tâm), và một thành phần song song, hay thành phần tiếp tuyến, làm thay đổi tốc độ.

Lực hướng tâm

II. Trắc nghiệm lực hướng tâm

Câu 1. Đại lượng nào sau đây không phải là đại lượng véctơ?

A. Động lượng.

B. Lực quán tính.

C. Công cơ học.

D. Xung của lực (xung lượng).

Câu 2. Phát biểu nào sau đây là đúng?

A. Khi vật chuyển động thẳng đều, công của hợp lực là khác không.

B. Trong chuyển động tròn đều, lực hướng tâm thực hiện công khác không,

C. Lực là đại lượng véctơ nên công cũng là vectơ.

D. Công của lực là đại lượng vô hướng và có giá trị đại số.

Câu 3. Một người nặng 60 kg leo lên một chiếc cầu thang. Trong 10 s người đó leo được 8 m tính theo phương thẳng đứng. Lấy g = 10m/s2 . Công suất mà người đó thực hiện được tính theo đơn vị mã lực HP (mã lực 1HP = 746W) là:

A. 480 HP. B. 2,10 HP. C. l,56 HP. D. 0,643 HP.

Câu 4: Một xạ thủ bắn tia từ xa với viên đạn có khối lượng 20g, khi viên đạn bay gân chạm tường thì có vận tốc 600 m/s, sau khi xuyên thủng bức tường vận tốc của viên đạn chỉ còn 200 m/s. Lực cản trung bình mà tường tác dụng lên viên đạn biết thời gian đạn xuyên qua tường (s) là

A. −2000 N. B. −8000 N. C. −4000 N. D. −6000 N.

Câu 5. Một hòn bi khối lượng 2 kg đang chuyển động với vận tốc 3m/s đến va chạm vào hòn bi có khối lượng 4kg đang nằm yên, sau va chạm hai viên bi gắn vào nhau và chuyến động cùng vận tốc. Độ lớn vận tốc của hai viên bi sau va chạm là:

A. 10 m/s. B. 15 m/s. C. 1 m/s. D. 5 m/s.

Câu 6. Một người công nhân có khối lượng 60kg nhảy ra từ một chiếc xe goòng có khối lượng 100kg đang chạy theo phương ngang với vận tốc 3 m/s, vận tốc nhảy của người đó đối với xe là 4 m/s. Độ lớn vận tốc của xe sau khi người công nhân nhảy cùng chiều với xe là:

A. 0,4 m/s. B. 0,8 m/s. C. 0,6 m/s. D. 0,5 m/s.

Câu 7. Một người công nhân có khối lượng 60kg nhảy ra từ một chiếc xe goòng có khối lượng 100kg đang chạy theo phương ngang với vận tốc 3 m/s, vận tốc nhảy của người đó đối với xe là 4 m/s. Độ lớn vận tốc của xe sau khi người công nhân nhảy ngược chiều với xe là:

A. 9 cm/s. B. 5,4 cm/s. C. 1 cm/s. D. 5cm/s.

Hy vọng rằng với những kiến thức mới về lý thuyết và bài tập về lực hướng tâm có đáp án trên đây, sẽ giúp bạn trả lời được các câu hỏi như lực hướng tâm có phải lực mới không hay tác hại của lực hướng tâm, bạn hoàn toàn có thể nắm chắc một cách dễ dàng và có những giờ học thư giãn!