Bài 41 trang 121 SGK Toán 8 tập 2

Đề bài

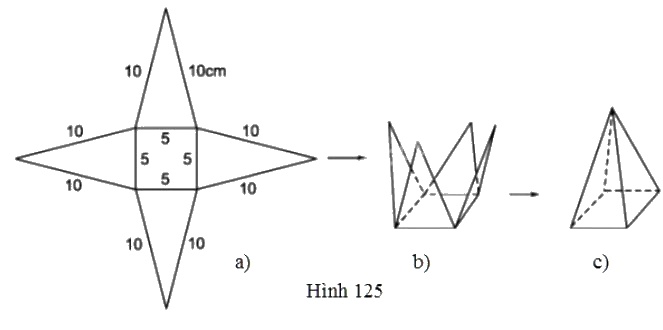
Vẽ cắt và gấp miếng bìa như đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.

a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?

b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.

c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu ?

Hướng dẫn giải

a) Trong hình 125a có 4 tam giác cân bằng nhau.

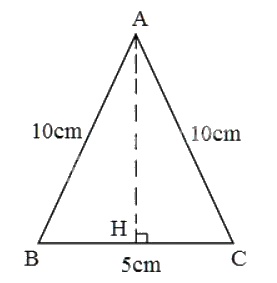
b) Chiều cao ứng với đáy của mỗi tam giác:

 \(AH = \sqrt{AC^{2}- HC^{2}}\)

 \(= \sqrt{AC^{2}- (\frac{BC}{2})^{2}}\)

 \(= \sqrt{10^{2}- (\frac{5}{2})^{2}} = \sqrt{100-\frac{25}{4}}= 9,68\) \(cm\)  

c) Diện tích xung quanh hình chóp:

        \(S_{xq} = p. d =\frac{1}{2}.5.4.9,68 = 96,8\) \( (cm^2) \) 

Diện tích đáy:

        \( S{đ} = 5^2 = 25 (cm^2) \) 

Diện tích toàn phần của hình chóp:

        \( S_ {tp} = S_{xq}+ S_{đ} = 96,8 + 25 = 121,8\) \((cm^2) \)