Bài 28 Vật lý lớp 11 - Lăng kính

Lăng kính là một bài nằm trong chương VII của môn Vật lý lớp 11. Cunghocvui sẽ tổng hợp lý thuyết và hướng dẫn giải bài tập một cách ngắn gọn bài Lăng kính Vật lý 11. Hy vọng tài liệu này sẽ giúp ích các bạn trong quá trình học tập môn Vật lý cấp Trung học phổ thông.

A. Tóm tắt lý thuyết Lăng kính

1. Khái niệm lăng kính

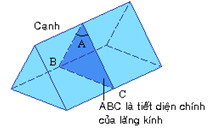
Lăng kính là một khối chất (thủy tinh, nhựa trong suốt) có dạng một hình lăng trụ đứng, đáy hình tam giác. Vì vậy người ta thường gọi là lăng kính tam giác. Lăng kính được dùng để khúc xạ, phản xạ và tán xạ ánh sáng sang màu quang phổ.

- Mặt bên của lăng kính bao gồm hai mặt phẳng giới hạn ở trên.

- Cạnh chung của hai mặt tiếp giáp nhau gọi là cạnh lăng kính

- Đáy là mặt đối diện với cạnh của lăng kính.

- Góc chiết quang hay góc ở đỉnh của lăng kính là hợp bởi hai mặt lăng kính.

Các yếu tố đặc trưng cho một lăng kính là chiết suất và góc chiết quang.

2. Đường truyền của ánh sáng qua lăng kính

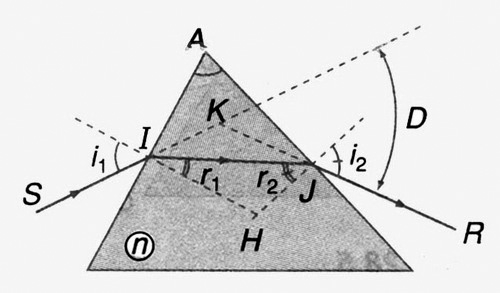
Chiều lệch của tia sáng:

- Nếu n > 1 thì lệch về phía đáy lăng kính

- Nếu n < 1 thì lệch về đỉnh lăng kính.

3. Các công thức lăng kính

- Sin\(i_1\) = n sin\(r_1\)

- Sin\(i_2\) = n sin\(r_2\)

- \(r_1\) + \(r_2\) = D

- D =  \(i_1\) + \(i_2\) - A

4. Lăng kính có tác dụng gì? Ứng dụng của lăng kính trong cuộc sống ngày nay

a, Máy quang phổ

- Lăng kính là một trong những thành phần chính của máy quang phổ

- Máy quang phổ phân tích ánh sáng từ nguồn phát ra các thành phần đơn sắc, từ đó xác định được cấu tạo của nguồn sáng.

b, Lăng kính phản xạ toàn phần

Là lăng kính được làm bằng thủy tinh. Lăng kính phản xạ toàn phần có tiết diện là một tam giác vuông cân. Nó có tác dụng dùng để điều chỉnh hướng đi của tia sáng hoặc ảnh thuận chiều (trong máy ảnh, ống nhòm).

B. Các dạng bài tập vận dụng Lăng kính vật lý 11

Dạng 1: Tính toán các đại lương liên quan đến lăng kính và vẽ đường đi của các tia sáng

Bài 1: Lăng kính có chiết suất n = \(\sqrt{2}\), góc chiết quang A = \(60^{0}\). Trong mặt bên AB của lăng kính, chiếu một chùm sáng đơn sắc hẹp với góc tới \(30^{0}\). Tính góc ló của tia sáng khi ra khỏi lăng kính và góc lệch của tia ló và tia tới?

Đáp số: Góc ló \(i_2\) = \(63,6^{0}\), góc lệch D = \(33,6^{0}\)

Bài 2: Cho A được ký hiệu là góc chiết quang. Mặt bên của lăng kính được chiếu tia sáng SI vuông góc đến. Góc được tạo bởi tia tới và tia ló là D = \(15^{0}\). Với chiết suất của lăng kính n = \(4\sqrt{3}\), tính góc chiết quang?

Đáp số: A = \(35,15^{0}\)

Bài 3: Tia sáng SI được chiếu vuông góc đến màn E tại điểm I. Trên đường chiếu của tia sáng, đặt đỉnh I của một lăng kính với góc chiết quang A = \(5^{0}\), chiết suất n = 1,5 với điều kiện SI vuông góc với mặt phân giác của góc chiết quang I, điểm J là tia sáng ló đến màn E. Biết khoảng cách từ màn đến đỉnh 1m, tính IJ?

Đáp án: IJ = 4,36cm

Bài 4: Lăng kính với tiết diện thẳng là tam giác vuông cân ABC, A = \(90^{0}\) đặt sao cho mặt nước trong chậu tiếp xúc với BC, nước có n = \(\dfrac{4}{3}\)

a, SI là một tia sáng đơn sắc được chiếu theo phương nằm ngang xuống mặt bên AB. Muốn tia sáng phản xạ toàn phần tại BC thì lăng kính có chiết suất N là bao nhiêu và khoảng cách từ A đến I?

b, Giả sử n = 1,41 và AI thỏa mãn điều kiện, vẽ đường đi của tia sáng?

Đáp số: n > 1,374

Dạng 2: Góc lệch cực tiểu

Bài 1: Một lăng kính với góc chiết quang A = \(60^{0}\), chiết suất n = 1,41 đặt trong không khí. Mặt bên được chiếu tia sáng SI với một góc tới i = \(45^{0}\)

a, Góc lệch của tia sáng qua lăng kính?

b, Góc lệch sẽ tăng hay giảm nếu góc tới được tăng hoặc giảm \(10^{0}\)

Đáp số: a, D = \(30^{0}\)

              b, D tăng

Bài 2: Lăng kính thủy tinh với góc chiết quang A, chiết suất n = 1,5. Qua lăng kính, chiếu tia sáng để góc chiết quang A bằng góc lệch cực tiểu. Biết rằng tam giác cân tại A là tiết diện thẳng, tính góc B?

Đáp số: B = \(48^{0}36'\)

Bài 3: Một lăng kính có chiết suất n = \( \sqrt{3}\), góc chiết quang A. Sau khi khúc xạ qua lăng kính, góc lệch cực tiểu của tia sáng đơn sắc cho tia ló đúng bằng A

a, Góc chiết quang A?

b, Lăng kính được nhúng vào nước với chiết suất n = \(\dfrac{4}{3}\), muốn có góc lệch cực tiểu thì góc tới i phải bằng bao nhiêu? Góc lệch cực tiểu khi đó bằng bao nhiêu?

Đáp số: a, \(60^{0}\)

             b, \(40,5^{0}\)

Bài 4: Tiết diện thẳng của một lăng kính là tam giác đều, chiết suất n = \(\sqrt{2}\) và được đặt trong môi trường không khí. Một tia sáng đơn sắc nằm trong một tiết diện thẳng được chiếu đến mặt bên của lăng kính và hướng từ đáy lên với góc tới i. Muốn góc lệch có giá trị cực tiểu \(D_{min}\) thì góc tới qua lăng kính phải bằng bao nhiêu? Tính \(D_{min}\)?

Đáp số: i = \(45^{0}\), \(D_{min}\)= \(30^{0}\)

Dạng 3: Điều kiện để có tia ló

Bài 1: Góc chiết quang của một lăng kính là A = \(30^{0}\), chiết suất n = 1,5. Tia sáng được chiếu dưới một góc tới i tới mặt lăng kính. Muốn tia sáng ló ra khỏi lăng kính thì i bằng bao nhiêu?

Đáp số: \(18^{0}10'\leq i \leq 21^{0}28'\)

Bài 2: Với A được ký hiệu là góc chiết quang của một lăng kính thủy tinh, chiết suất n = 1,41. Tia sáng SI với góc tới i được chiếu đến lăng kính tại I. Tính giá trị của i để:

a, Góc lệch cực tiểu được có từ tia sáng SI?

b, Tia ló không tồn tại?

Đáp số: a, i = \(45^{0}\)

             b, i \(\leq 21^{0}28'\)

Bài 3: Tiết diện thẳng của một lăng kính là tam giác đều ABC, chiết suất n = 1,5. Tại mặt bên AB, chiếu một tia sáng đơn sắc tại I và góc tới i, thay đổi được. Muốn để có tia ló ở mặt AC, hãy xác định khoảng biến thiên của i?

Đáp số:  \(28^{0}\leq i\leq 90^{0}\)

4. Một số bài tập trắc nghiệm

Câu 1: Trong mặt bên của một lăng kính có tiết diện là một tam giác cân ABC có góc chiết quang A = \(8^{0}\), chiếu một chùm tia sáng với theo phương vuông góc với mặt phẳng phân giác của góc chiết quang tại một điểm tới rất gần A. Góc lệch của tia ló so với tia tới là bao nhiêu khi biết chiết suất của lăng kính với tia đó là n = 1,5:

a. \(2^{0}\)                                b. \(4^{0}\)                              c. \(8^{0}\)                          d. \(12^{0}\)

Câu 2: A = \(60^{0}\) là góc chiết quang của một lăng kính, chiết suất n = \(\sqrt{2}\) trong điều kiện không khí. Tia sáng tới mặt thứ nhất với góc tới i, mặt thứ hai có tia ló khi:

a.  \(i\leq 15^{0}\)                       b. \(i\leq 20^{0}\)                     c. \(i\leq 21^{0}47'\)             d. \(i\geq 21^{0}47'\)

Câu 3: Lăng kính có góc chiết quang và chiết suất n = \(\sqrt{3}\). Góc lệch có giá trị cực tiểu \(D_{min}\) khi ở trong không khí bằng:

a. \(30^{0}\)                             b. \(60^{0}\)                           c. \(45^{0}\)                         d. Tất cả đều sai

Câu 4: Trong mặt bên của lăng kính tam giác vuông, một tia sáng được chiếu tới dưới một góc tới \(45^{0}\). Chiết suất nhỏ nhất của lăng kính là bao nhiêu để không có tia ló ra mặt bên kia:

a.\(\dfrac{\sqrt{2}+1}{2}\)                      b. \(\sqrt{\dfrac{3}{2}}\)                         c. \(\dfrac{\sqrt{2}}{2}\)                        d. \(\sqrt{2} +1\)

Câu 5: Trong phân giác của lăng kính dạng tam giác đều, một tia sáng được chiếu thẳng góc, chiết suất n = \(\sqrt{2} \). Giá trị của góc lệch D là:

a. \(30^{0}\)                           b. \(45^{0}\)                           c. \(60^{0}\)                          d. \(33,6^{0}\)

 Đáp án một số câu trắc nghiệm bài 28 Vật lý 11: 

Câu	Câu 1	Câu 2	Câu 3	Câu 4	Câu 5
Đáp án	B	C	A	B	D

Tham khảo thêm >>> Bài tập Bài 28 Sách giáo khoa - Lăng kính

Với bài Lăng kính Vật lý 11, Cunghocvui đã gửi tới các bạn bài viết tóm tắt lý thuyết và các dạng bài tập đầy đủ nhất. Nếu có thắc mắc gì về lăng kính 3D, hãy để lại comment dưới phần bình luận nhé!