Bài 18 trang 105 SGK Toán 8 tập 2

Đề bài

Đố: Các kích thước của một hình hộp chữ nhật là \(4cm,\; 3cm,\;  2cm\). Một con kiến bò theo mặt của hình hộp đó từ \(Q\) đến \(P\) (h.92):

a) Hỏi con kiến bò theo đường nào là ngắn nhất?

b) Độ dài ngắn nhất đó bằng bao nhiêu xentimét?

Hướng dẫn giải

a) Vì con kiến bò theo mặt của hình hộp từ \(Q\) đến \(P\) tức phải bò trên “ một mặt phẳng” ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:

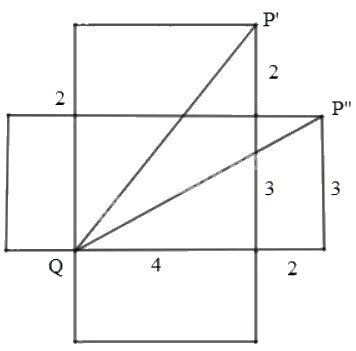
Khi đó, \(P\) sẽ có hai vị trí là \(P’\) và \(P’’\) và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng \(QP’ \) và \(QP’’\) Ta có:

Hình chữ nhật với chiều dài \(2+3=5cm\) và chiều rộng \( 4cm\) có đường chéo \(QP’\) với độ dài: 

                   \(QP’ = \sqrt{4^{2}+ 5^{2}} =\sqrt{41}cm \) 

Hình chữ nhật với chiều dài \(4+2=6cm\) và chiều rộng \( 3cm\) có đường chéo \(QP’\) với độ dài: 

                  \(QP’’ = \sqrt{4^{2}+ 5^{2}}=\sqrt{45}cm \) 

Ta có : \( \sqrt{41} < \sqrt{45} \) . Vậy đường đi ngắn nhất là  \(QP’\)

b) Vậy độ dài ngắn nhất là \( \sqrt{41} \approx 6,4 cm\) .